题目内容
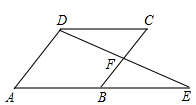
如图，在△ABC中，E是BC上的一点，EC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF-S△BEF=（ ）
| A．1 | B．2 | C．3 | D．4 |
B
试题分析：∵点D是AC的中点，
∴AD=
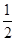AC，∵S△ABC=12，
∴S△ABD=
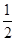S△ABC=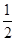×12=6．∵EC=2BE，S△ABC=12，
∴S△ABE=
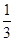S△ABC=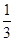×12=4，∵S△ABD-S△ABE=（S△ADF+S△ABF）-（S△ABF+S△BEF）=S△ADF-S△BEF，
即S△ADF-S△BEF=S△ABD-S△ABE=6-4=2．
故选B．
练习册系列答案
相关题目
