题目内容
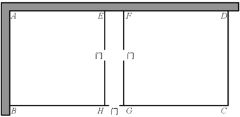
【题目】某农场要建一个饲养场（矩形ABCD）两面靠现有墙（AD位置的墙最大可用长度为27米，AB位置的墙最大可用长度为15米），另两边用木栏围成，中间也用木栏隔开，分成两个场地及一处通道，并在如图所示的三处各留1米宽的门（不用木栏）。建成后木栏总长45米。设饲养场（矩形ABCD）的一边AB长为x米.
（1）饲养场另一边BC= 米（用含x的代数式表示）.
（2）若饲养场的面积为180平方米，求x的值.
【答案】（1）（48-3x）；（2）10.
【解析】
（1）设饲养场（矩形ABCD）的一边（AB）长为x米，得出EH、FG所用围栏长均为（x-1）米，CD=x米，BC=45-（x+x-1+x-1）+1=48-3x（米），
（2）根据矩形面积公式可得方程；解方程即可得答案．而AB和AD长限制了x的取值.
解：（1）设饲养场（矩形ABCD）的一边（AB）长为x米，得出EH、FG所用围栏长均为（x-1）米，CD=x米，BC=45-（x+x-1+x-1）+1=48-3x（米），
练习册系列答案
赢在课堂名师课时计划系列答案
天天向上课时同步训练系列答案
阳光课堂同步练习系列答案
相关题目
【题目】一种树苗，栽种时高度约为80厘米，为研究它的生长情况，测得数据如下表：
（1）此变化过程中_____是自变量，_____是因变量；
（2）树苗高度h与栽种的年数n的关系式为_____；
（3）栽种后_____后，树苗能长到280厘米．
栽种以后的年数n/年 | 高度h/厘米 |
1 | 105 |
2 | 130 |
3 | 155 |
4 | 180 |
… | … |
