题目内容
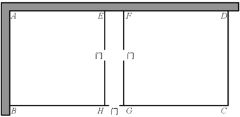
【题目】已知:如图在△ABC,△ADE中,∠BAC=∠DAE=90°,AB=AC,AD=AE,点C,D,E三点在同一条直线上,连接BD,BE.以下四个结论:
①BD=CE;②BD⊥CE;③∠ACE+∠DBC=45°;④BE2=2(AD2+AB2),
其中结论正确的个数是

A.1 B.2 C.3 D.4
【答案】C
【解析】
试题①∵∠BAC=∠DAE=90°,∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE。
∵在△BAD和△CAE中,AB=AC,∠BAD=∠CAE,AD=AE,
∴△BAD≌△CAE(SAS)。∴BD=CE。本结论正确。
②∵△BAD≌△CAE,∴∠ABD=∠ACE。
∵∠ABD+∠DBC=45°,∴∠ACE+∠DBC=45°。∴∠DBC+∠DCB=∠DBC+∠ACE+∠ACB=90°。
∴BD⊥CE。本结论正确。
③∵△ABC为等腰直角三角形,∴∠ABC=∠ACB=45°。∴∠ABD+∠DBC=45°。
∵∠ABD=∠ACE,∴∠ACE+∠DBC=45°。本结论正确。
④∵BD⊥CE,∴在Rt△BDE中,利用勾股定理得:BE2=BD2+DE2。
∵△ADE为等腰直角三角形,∴DE=![]() AD,即DE2=2AD2。
AD,即DE2=2AD2。
∴BE2=BD2+DE2=BD2+2AD2。
而BD2≠2AB2,本结论错误。
综上所述,正确的个数为3个。故选C。

练习册系列答案
相关题目
【题目】探索与应用.先填写下表,通过观察后再回答问题:
a | … | 0.0001 | 0.01 | 1 | 100 | 10000 | … |
| … | 0.01 | x | 1 | y | 100 | … |
(1)表格中x= ;y= ;
(2)从表格中探究a与![]() 数位的规律,并利用这个规律解决下面两个问题:
数位的规律,并利用这个规律解决下面两个问题:
①已知![]() ≈3.16,则
≈3.16,则![]() ≈ ;②已知
≈ ;②已知![]() =1.8,若
=1.8,若![]() =180,则a= ;
=180,则a= ;
(3)拓展:已知![]() ,若
,若![]() ,则b= .
,则b= .