题目内容
如图,在矩形ABCD(AB<AD)中,将△ABE沿AE对折,使AB边落在对角线AC上,点B的对应点为F,同时将△CEG沿EG对折,使CE边落在EF所在直线上,点C的对应点为H.

(1)证明:AF∥HG(图(1));
(2)如果点C的对应点H恰好落在边AD上(图(2)).判断四边形AECH的形状,并说明理由.

(1)证明:AF∥HG(图(1));
(2)如果点C的对应点H恰好落在边AD上(图(2)).判断四边形AECH的形状,并说明理由.
(1)由轴对称性质可得∠AFE=∠B=90°,∠H=∠BCD=90°,问题得证;(2)菱形
试题分析:(1)由轴对称性质可得∠AFE=∠B=90°,∠H=∠BCD=90°,问题得证;
(2)根据平行线的性质可得∠AEB=∠DAE,再结合∠AEB=∠AEH可得∠DAE=∠AEH,即可证得AH=EH,由EC=EH可得AH=EC,再结合AH∥EC,AC⊥EH即可证得结论.
(1)由对折(轴对称)性质可得:∠AFE=∠B=90°,∠H=∠BCD="90°"
∴∠AFH=∠AFE=∠H
∴AF∥HG
(2)四边形 AECH是菱形.理由如下:
∵AD∥BC
∴∠AEB=∠DAE
∵∠AEB=∠AEH
∴∠DAE=∠AEH
∴AH=EH
∵EC=EH
∴AH="EC"
∵AH∥EC,AC⊥EH
∴四边形 AECH是菱形.
点评:特殊四边形的判定和性质是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.

练习册系列答案
相关题目

 中,
中, //
// ,对角线
,对角线 、
、 相交于点
相交于点 ,
, ,
, ,
, ,则
,则 .
.


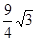


 中,
中, ,
, 为垂足.若
为垂足.若 ,则
,则 ( )
( )




 ,DB="4," 求四边形ABCD的面积.
,DB="4," 求四边形ABCD的面积.
 ,则菱形ABCD的面积是__________
,则菱形ABCD的面积是__________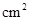 .
.
 ,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③
,折叠正方形ABCD,使AD落在BD上,点A恰好与BD上的点F重合,展平后,折痕DE分别交AB,AC于点E,G,连接GF,下列结论:①AE=AG;②tan∠AGE=2;③ ;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。
;④四边形ABFG为等腰梯形;⑤BE=2OG,则其中正确的结论个数为( )。