��Ŀ����
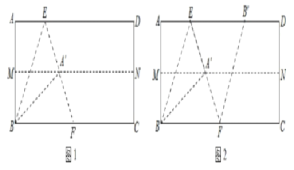
����Ŀ����һ�ž���ֽƬABCD�����۵�������������£�
��һ�����ȶ��ۣ�ʹAD��BC�غϣ��õ��ۺ�MN��չ����
�ڶ�������һ���۵���ʹ��A����MN�ĵ�A�䴦����ʹ�ۺ۾�����B���õ��ۺ�BE��ͬʱ���õ��߶�BA�䣬EA�䣬չ������ͼ1��
������������EA�����ڵ�ֱ���۵�����B����AD�ĵ�B�䴦���õ��ۺ�EF��ͬʱ�õ��߶�B��F��չ������ͼ2��
��1��֤������ABE=30�㣻
��2��֤�����ı���BFB��EΪ���Σ�
���𰸡�������
��������
��1�����ݵ�M��AB���е��жϳ�A����EF���е㣬Ȼ���жϳ�BA����ֱƽ��EF�������߶δ�ֱƽ�����ϵĵ㵽���˵�ľ�����ȿɵ�BE=BF���ٸ��ݵ������������ߺ�һ�����ʿɵá�A��BE=��A��BF�����ݷ��۵����ʿɵá�ABE=��A��BE��Ȼ����ݾ��ε��ĸ��Ƕ���ֱ�Ǽ��㼴�ɵ�֤��
��2�����ݷ��۱任�����ʿɵ�BE=B��E��BF=B��F��Ȼ�����BE=B��E=B��F=BF���ٸ��������߶���ȵ��ı���������֤����
(1)�߶���AD��BC�غϣ��ۺ���MN��
���M��AB���е㣬
��A����EF���е㣬
�ߡ�BA��E=��A=90����
��BA����ֱƽ��EF��
��BE=BF��
���A��BE=��A��BF��
�ɷ��۵�����,��ABE=��A��BE��
���ABE=��A��BE=��A��BF��
���ABE=![]() ��90��=30����
��90��=30����
(2)����EA�����ڵ�ֱ���۵�,��B����AD�ϵĵ�B������
��BE=B��E,BF=B��F��
��BE=BF��
��BE=B��E=B��F=BF��
���ı���BFB��EΪ���Ρ�