题目内容
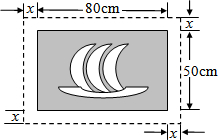
在一幅长80cm，宽50cm的矩形风景画的四周镶一条金色纸边，制成一幅矩形挂图，如图所示，如果要使整个挂图的面积是5400cm2，设金色纸边的宽为xcm，那么x满足的方程是______．并求出金色纸边的宽度．
A．x2+130x-1400=0；B．x2+65x-350=0；
C．x2-130x-1400=0；D．x2-65x-350=0．
A．x2+130x-1400=0；B．x2+65x-350=0；
C．x2-130x-1400=0；D．x2-65x-350=0．
∵挂图的长为（80+2x）cm，宽为（50+2x）cm，
∴可列方程为（80+2x）×（50+2x）=5400，
化简得x2+65x-350=0，
解得：x=-70或x=5，
∴金色纸边的宽度为5cm．
故选B．
∴可列方程为（80+2x）×（50+2x）=5400，
化简得x2+65x-350=0，
解得：x=-70或x=5，
∴金色纸边的宽度为5cm．
故选B．
练习册系列答案
相关题目
边向点C以2cm/s的速度移动．
