题目内容
【题目】如图,为了拆除震后危楼,抗震减灾工作组对所剩部分危楼楼房进行摸排测量.在危楼楼角B点处,测得危楼楼顶A的仰角为60°;沿楼角B点的正前方前进8米到达点C,在离C点2米高的D处测得危楼楼顶A的仰角为30°.请根据以上测量数据,求出楼顶A离地面的高度.(![]() ≈1.7,精确到1米)
≈1.7,精确到1米)
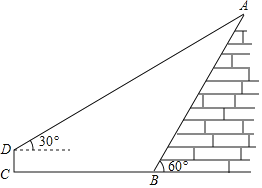
【答案】楼顶A离地面的高度约为10米.
【解析】
作AE⊥CB交CB的延长线于E,作DF⊥AE于F,设BE=x,根据正切的定义用x分别表示出AE、DF,根据正切的定义列出方程,解方程求出x,根据题意求出AE.
作AE⊥CB交CB的延长线于E,作DF⊥AE于F,
则四边形DCEF为矩形,
∴EF=CD=2,DF=CE,
设BE=x,则DF=CE=8+x,
在Rt△ABE中,tan∠ABE![]() ,
,
则AE=BEtan∠ABE![]() x,
x,
在Rt△ADF中,tan∠ADF![]() ,
,
则![]() ,
,
解得:x=4![]() ,
,
∴AE![]() x=4
x=4![]() 3≈10(米).
3≈10(米).
答:楼顶A离地面的高度约为10米.


练习册系列答案
相关题目