题目内容
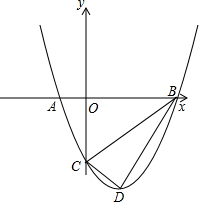
 如图,抛物线与x轴交于A、B两点,以线段AB为直径的半圆与抛物线在第二象限的交点为C,与y轴交于D点,设∠BCD=α,则
如图,抛物线与x轴交于A、B两点,以线段AB为直径的半圆与抛物线在第二象限的交点为C,与y轴交于D点,设∠BCD=α,则 的值为
的值为
- A.sin2α
- B.cos2α
- C.tan2α
- D.tan-2α
C
分析:首先连接AD,BD,由圆周角定理可得∠BAD=∠BCD=α,又由AB是半圆的直径,可得∠ADB=90°,然后根据同角的余角相等,求得∠ODB=∠BAD=α,再利用三角函数的定义,求得OB与OA,继而可求得 的值.
的值.
解答: 解:连接AD,BD,
解:连接AD,BD,
∵∠BAD与∠BCD是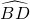 对的圆周角,
对的圆周角,
∴∠BAD=∠BCD=α,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠ODB+∠OBD=90°,
∴∠ODB=∠BAD=α,
在Rt△AOD中,AO=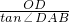 =
= ,
,
在Rt△BOD中,OB=OD•tan∠ODB=OD•tanα,
∴ =
= =tan2α.
=tan2α.
故选C.
点评:此题考查了圆周角定理、直角三角形的性质以及三角函数的知识.此题综合性较强,难度较大,解题的关键是准确作出辅助线,利用数形结合思想求解.
分析:首先连接AD,BD,由圆周角定理可得∠BAD=∠BCD=α,又由AB是半圆的直径,可得∠ADB=90°,然后根据同角的余角相等,求得∠ODB=∠BAD=α,再利用三角函数的定义,求得OB与OA,继而可求得
 的值.
的值.解答:
 解:连接AD,BD,
解:连接AD,BD,∵∠BAD与∠BCD是
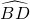 对的圆周角,
对的圆周角,∴∠BAD=∠BCD=α,
∵AB是半圆的直径,
∴∠ADB=90°,
∴∠BAD+∠ABD=90°,
∵∠ODB+∠OBD=90°,
∴∠ODB=∠BAD=α,
在Rt△AOD中,AO=
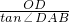 =
= ,
,在Rt△BOD中,OB=OD•tan∠ODB=OD•tanα,
∴
 =
= =tan2α.
=tan2α.故选C.
点评:此题考查了圆周角定理、直角三角形的性质以及三角函数的知识.此题综合性较强,难度较大,解题的关键是准确作出辅助线,利用数形结合思想求解.

练习册系列答案
相关题目
 如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.
如图,抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,-3),设抛物线的顶点为D.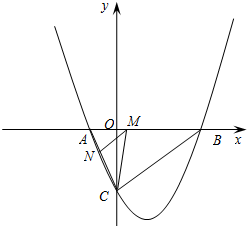 如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根.
如图,抛物线与x轴交于A(x1,0)、B(x2,0)两点,且x1<x2,与y轴交于点C(0,-4),其中x1,x2是方程x2-4x-12=0的两个根. (2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是
(2012•历下区一模)如图,抛物线与x轴交于A(-1,0),B(4,0)两点,与y轴交于C(0,3),M是抛物线对称轴上的任意一点,则△AMC的周长最小值是 如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.
如图,抛物线与y轴交于点A(0,4),与x轴交于B、C两点.其中OB、OC是方程的x2-10x+16=0两根,且OB<OC.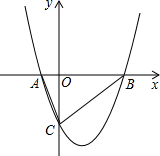 如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).
如图,抛物线与x轴交于A、B(6,0)两点,且对称轴为直线x=2,与y轴交于点C(0,-4).