题目内容
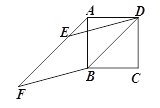
【题目】如图,以正方形ABCD的对角线BD为边作菱形BDEF,当点A,E,F在同一直线上时,∠F的正切值为___________.
【答案】![]()
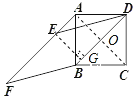
【解析】连接BD与AC相交于O,过点E作EG⊥BD于G,可得四边形AOEG是矩形,可得GE=AO,再根据直角三角形30°所对的直角边等于斜边的一半,求出∠EDG=30°即可求出答案.
证明:连接AC交BD于O,过点E作EG⊥BD于G;
∵正方形ABCD
∴∠ACB=∠DBC=45°,AC=BD=2BO,∠BOC=90°,
∵菱形AEFC,∠F=∠DB,∠DEF=180°-∠F,
∴EF=BF,BD∥EF,
∴∠BAF=∠DBA=45°,
∴∠CAF=∠BAC+∠BAF=90°,
∵EG⊥BD,
∴四边形AOEG是矩形,
∴GE=AO,
∴DE=2GE,
∴∠EDG=30°,
∴∠F=30°
∴∠F的正切值为![]() .
.
“点睛”本题考查了正方形的性质,矩形的判定与性质,菱形的性质,直角三角形30°所对的直角边等于斜边的一半的性质,作辅助线构造出矩形的和30°的直角三角形是解题的关键.

 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可随机抽取一张奖券,抽得奖券“紫气东来”、“花开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元。小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:
奖券种类 | 紫气东来 | 花开富贵 | 吉星高照 | 谢谢惠顾 |
出现张数(张) | 500 | 1000 | 2000 | 6500 |
(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物卷,哪种方式更合算?并说明理由。
【题目】已知甲、乙两种水稻实验品种连续5年的平均单位面积产量如下(单位:吨/公顷)
品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5年 |
甲 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
乙 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
经计算,甲乙的平均数均为10,试根据这组数据估计 种水稻品种的产量较稳定.