题目内容
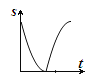
【题目】已知一次函数y=mx+n﹣2的图象如图所示,则m、n的取值范围是( )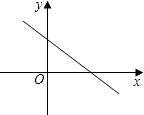
A.m>0,n<2
B.m>0,n>2
C.m<0,n<2
D.m<0,n>2
【答案】D
【解析】解:∵一次函数y=mx+n﹣2的图象过二、四象限,
∴m<0,
∵函数图象与y轴交于正半轴,
∴n﹣2>0,
∴n>2.
故选D.
【考点精析】解答此题的关键在于理解一次函数的概念的相关知识,掌握一般地,如果y=kx+b(k,b是常数,k不等于0),那么y叫做x的一次函数,以及对一次函数的图象和性质的理解,了解一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远.

练习册系列答案
 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
【题目】某公司销售部有营销人员20人,销售部为了制定某种商品的月销售额,统计了这20人的销售额如下:
销售额(万元) | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
频数(个) | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 |
(1)求这20位营销人员月销售额的平均数、中位数;
(2)假设你是销售部负责人,你认为把每位营销人员的月销售额定为多少合适?请说明你的理由.