题目内容
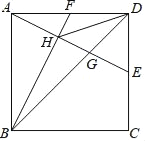
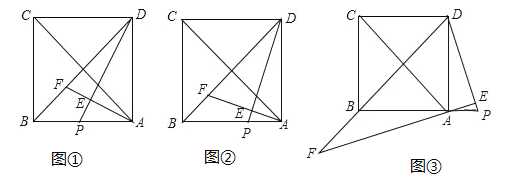
【题目】如图,在边长为6的正方形ABCD中,点P为AB上一动点,连接DB、DP,AE⊥DP于E.
(1)如图①,若P为AB的中点,则![]() = ;
= ;![]() = ;
= ;
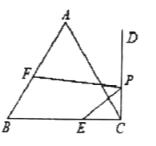
(2)如图②,若![]() 时,证明:AC=4BF;
时,证明:AC=4BF;
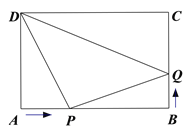
(3)如图③,若P在BA的延长线上,当![]() = 时,
= 时,![]() .
.
【答案】(1)![]() ,
,![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]() .
.
【解析】
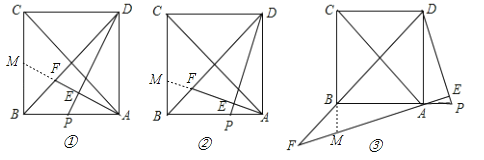
(1)延长AF交BC于M,证△ABM≌△DAP,得BM=AP,再根据△MBF∽△ADF对应边成比例列出比例式![]() =
=![]() ,然后再根据正方形的边长相等,对角线相等进行转化即可求解;
,然后再根据正方形的边长相等,对角线相等进行转化即可求解;
(2)先根据已知条件求出![]() =
=![]() ,然后同(1)的方法作出辅助线即可进行证明;
,然后同(1)的方法作出辅助线即可进行证明;
(3)同前两小题的思路,延长CB交AF于点M,然后同(1)的求解思路进行求解计算.
(1)延长AF交BC于M,∴∠BAM+∠AMB=90°.
∵AE⊥DP,∴∠BAM+∠DPA=90°,∴∠AMB=∠DPA.
在△ABM和△DAP中,∵ ,∴△ABM≌△DAP(AAS),∴AP=BM(全等三角形对应边相等).
,∴△ABM≌△DAP(AAS),∴AP=BM(全等三角形对应边相等).
∵四边形ABCD是正方形,∴BC∥AD,∴△MBF∽△ADF,∴![]() =
=![]() .
.
∵点P是AB的中点,∴AP=BM=![]() AB=
AB=![]() AD,∴
AD,∴![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() .
.
又∵AC=BD,∴![]() =
=![]() .
.
故答案为:![]() ;
;
(2)∵![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() ,方法同(1),延长AF交BC于M,则
,方法同(1),延长AF交BC于M,则![]() =
=![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() .
.
∵正方形的对角线AC=BD,∴![]() =
=![]() ,∴AC=4BF;
,∴AC=4BF;
(3)延长CB交AF于点M,方法同(1)可得:![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,即
,即![]() =
=![]() .
.
∵正方形的对角线AC=BD,∴![]() =
=![]() .
.
故答案为:![]() .
.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目