题目内容
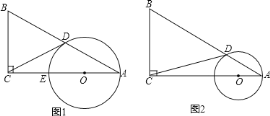
【题目】如图,![]() 的半径长为
的半径长为![]() ,
,![]() 垂直弦
垂直弦![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() ,与过点
,与过点![]() 的
的![]() 的切线交于点
的切线交于点![]() ,已知
,已知![]() .
.
![]() 若
若![]() ,求
,求![]() 、
、![]() 的长;
的长;
![]() 求
求![]() 的最大值.
的最大值.
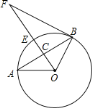
【答案】(1)![]() ;(2)
;(2)![]() 的最大值为
的最大值为![]() .
.
【解析】
(1)利用切线的性质以及勾股定理得出AB的长,进而利用△BOC∽△OBF,得出即可;
(2)首先得出△BCO∽△FCB,进而用x表示出FC的长,即可利用二次函数最值求法得出即可.
(1)EC=2,则CO=5﹣2=3.
∵CO⊥AB,∴AB=2CB.在Rt△BCO中,BO=5,∴BC=![]() =
=![]() =4,∴AB=8.
=4,∴AB=8.
∵BF为⊙O的切线,∴OB⊥BF.
在△BOC和△OBF中,∵∠OCB=∠FBO=90°,∠BOC=∠BOF,∴△BOC∽△OBF,∴![]() =
=![]() ,∴
,∴![]() =
=![]() ,解得:BF=
,解得:BF=![]() ;
;
(2)∵∠CBF+∠OBC=90°,∠BOC+∠OBC=90°,∴∠CBF=∠BOC,又∠BCF=∠BCO=90°,∴△BCO∽△FCB,∴![]() =
=![]() ,∴BC2=OC×FC.
,∴BC2=OC×FC.
∵OC=5﹣x,OB=5,∴BC2=BO2﹣CO2=25﹣(5﹣x)2,∴25﹣(5﹣x)2=CO×FC=(5﹣x)×FC,∴FC=![]() ,∴EF×CO2=(FC﹣EC)×CO2
,∴EF×CO2=(FC﹣EC)×CO2
=(![]() ﹣x)(5﹣x)2=5x(5﹣x)=﹣5(x﹣
﹣x)(5﹣x)2=5x(5﹣x)=﹣5(x﹣![]() )2+
)2+![]()
∴EF×CO2的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目