题目内容
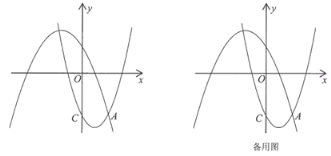
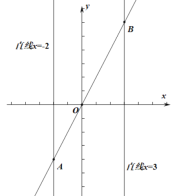
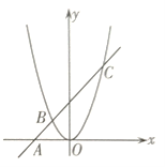
【题目】如图,在平面直角坐标系中,一次函数![]() 与
与![]() 轴交于点
轴交于点![]() ,与二次函数交于点
,与二次函数交于点![]() 、点
、点![]() ,点
,点![]() 三点的横坐标分别是
三点的横坐标分别是![]() ,则下面四个等式中不一定成立的是( )
,则下面四个等式中不一定成立的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
【答案】A
【解析】
先设抛物线为![]() ,然后与一次函数联立方程,根据一元二次方程根与系数的关系可得
,然后与一次函数联立方程,根据一元二次方程根与系数的关系可得![]() ,
,![]() ,再根据点A(a,0)在一次函数
,再根据点A(a,0)在一次函数![]() 图像上可得
图像上可得![]() ,由此可得
,由此可得![]() ,再根据所给选项进行变形,能够得到
,再根据所给选项进行变形,能够得到![]() 便是正确选项,由此可求得答案.
便是正确选项,由此可求得答案.
解:设抛物线为![]() ,
,
将![]() 与
与![]() 联立方程得
联立方程得![]() ,
,
∴![]() ,
,
∵交点![]() 两点的横坐标分别是
两点的横坐标分别是![]() ,
,
∴![]() 与
与![]() 是方程
是方程![]() 的两个解,
的两个解,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∵点A(a,0)在一次函数![]() 图像上,
图像上,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() ,
,
B、若![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∴![]() ,故选项B正确;
,故选项B正确;
C、若![]() ,
,
则![]() ,
,
∴![]() ,
,
∴![]()
∴![]()
∵![]() ,
,
∴![]()
∴![]() ,故选项C正确;
,故选项C正确;
D、若![]() ,
,
则![]()
∴![]() ,故选项D正确;
,故选项D正确;
故选:A

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】已知二次函数 y=ax2+bx+c,其中 y 与 x 的部分对应值如表:
x | -2 | -1 | 0.5 | 1.5 |
y | 5 | 0 | -3.75 | -3.75 |
下列结论正确的是( )
A.abc<0B.4a+2b+c>0
C.若 x<-1 或 x>3 时,y>0D.方程 ax2+bx+c=5 的解为 x1=-2,x2=3
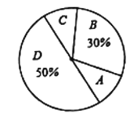
【题目】研究机构对本地区18-20岁的大学生就某个问题做随机调查,要求被调查者从A、B、C、D四个选项中选择自己赞同的一项,并将结果绘制成两幅不完整的统计图(如图):
大学生就某个问题调查结果统计表 | 大学生就某个问题调查结果扇形统计图 | ||||||||||||
|
|
请结合图中信息解答以下问题:
(1)m=_____,b=_____.
(2)若该地区18~20岁的大学生有1.2万人,请估计这些大学生中选择赞同A选项的人数:
(3)该研究机构决定从选择“C”的人中随机抽取2名进行访谈,而选择“C”的这4人中只有一名男性,求这名男性刚好被抽取到的概率.