题目内容
如图,在平行四边形ABCD中,AB=5,BC=10,F为AD的中点,CE⊥AB于E,设∠ABC=α(60°≤α<90°).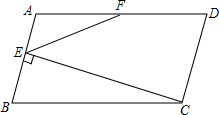
(1)当α=60°时,求CE的长;
(2)当60°<α<90°时,
①是否存在正整数k,使得∠EFD=k∠AEF?若存在,求出k的值;若不存在,请说明理由.
②连接CF,当CE2-CF2取最大值时,求tan∠DCF的值.
(1) 5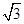 ;(2) k=3,
;(2) k=3,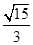 .
.
解析试题分析:(1)利用60°角的正弦值列式计算即可得解;
(2)①连接CF并延长交BA的延长线于点G,利用“角边角”证明△AFG和△DFC全等,根据全等三角形对应边相等可得CF=GF,AG=CD,再利用直角三角形斜边上的中线等于斜边的一半可得EF=GF,再根据AB、BC的长度可得AG=AF,然后利用等边对等角的性质可得∠AEF=∠G=∠AFG,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠EFC=2∠G,然后推出∠EFD=3∠AEF,从而得解;
②设BE=x,在Rt△BCE中,利用勾股定理表示出CE2,表示出EG的长度,在Rt△CEG中,利用勾股定理表示出CG2,从而得到CF2,然后相减并整理,再根据二次函数的最值问题解答.
试题解析:(1)∵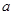 =60°,BC=10,
=60°,BC=10,
∴sin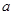 =
=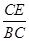 ,
,
即sin60°=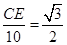 ,解得CE=5
,解得CE=5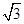 ;
;
(2)①存在k=3,使得∠EFD=k∠AEF.理由如下:
连接CF并延长交BA的延长线于点G,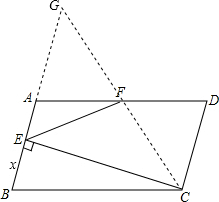
∵F为AD的中点,
∴AF=FD,
在平行四边形ABCD中,AB∥CD,
∴∠G=∠DCF,
在△AFG和△DFC中,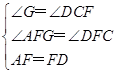 ,
,
∴△AFG≌△DFC,
∴CF=GF,AG=CD,
∵CE⊥AB,
∴EF=GF,
∴∠AEF=∠G,
∵AB=5,BC=10,点F是AD的中点,
∴AG=5,AF=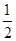 AD=
AD=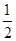 BC=5,
BC=5,
∴AG=AF,
∴∠AFG=∠G,
在△EFG中,∠EFC=∠AEF+∠G=2∠AEF,
又∵∠CFD=∠AFG,
∴∠CFD=∠AEF,
∴∠EFD=∠EFC+∠CFD=2∠AEF+∠AEF=3∠AEF,
因此,存在正整数k=3,使得∠EFD=3∠AEF;
②设BE=x,∵AG=CD=AB=5,
∴EG=AE+AG=5-x+5=10-x,
在Rt△BCE中,CE2=BC2-BE2=100-x2,
在Rt△CEG中,CG2=EG2+CE2=(10-x)2+100-x2=200-20x,
∵由①知CF=GF,
∴CF2=(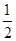 CG)2=
CG)2= CG2=
CG2= (200-20x)=50-5x,
(200-20x)=50-5x,
∴CE2-CF2=100-x2-50+5x=-x2+5x+50=-(x-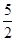 )2+50+
)2+50+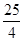 ,
,
∴当x=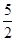 ,即点E是AB的中点时,CE2-CF2取最大值,此时,EG=10-x=10-
,即点E是AB的中点时,CE2-CF2取最大值,此时,EG=10-x=10-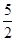 =
=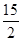 ,
,
CE=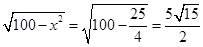 ,
,
所以,tan∠DCF=tan∠G=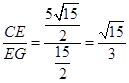
考点: 1.平行四边形的性质;2.二次函数的最值;3.勾股定理.


 (单位:
(单位: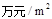 )与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为
)与月份x(6≤x≤11,x为整数)之间满足一次函数关系,每月的销售面积为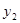 (单位:
(单位: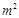 ),其中y2=-2000x+26000(6≤x≤11,x为整数).
),其中y2=-2000x+26000(6≤x≤11,x为整数). 的函数关系式;
的函数关系式;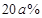 ,于是决定将12月份的销售价格在11月的基础上增加
,于是决定将12月份的销售价格在11月的基础上增加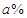 ,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为
,该计划顺利完成.为了尽快收回资金,2014年1月公司进行降价促销,该月销售额为(1500+600a)万元.这样12月、1月的销售额共为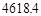 万元,请根据以上条件求出
万元,请根据以上条件求出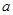 的值为多少?
的值为多少?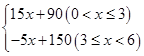 若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=
若在国外销售,平均每件产品的利润y2(元)与国外的销售数量t(千件)的关系为: y2=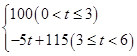
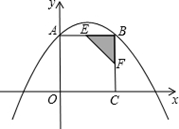
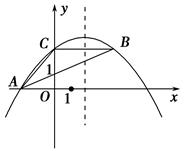
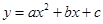 经过点A、B和D(4,
经过点A、B和D(4,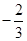 ).
).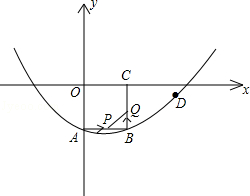
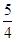 时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.
时,在抛物线上是否存在点R,使得以点P、B、Q、R为顶点的四边形是平行四边形?如果存在,求出R点的坐标;如果不存在,请说明理由.