Question

【题目】问题提出

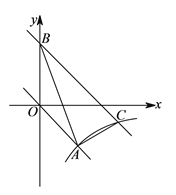
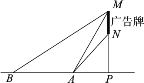
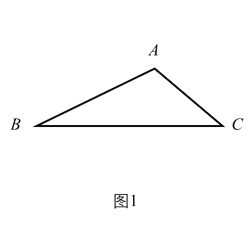
（1）如图（1），已知中，，，，求点到的最短距离．

问题探究

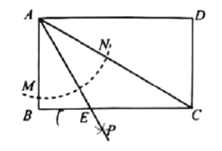
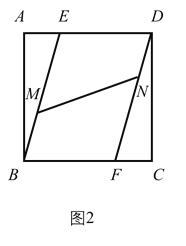
（2）如图（2），已知边长为3的正方形，点、分别在边和上，且，，连接、，若点、分别为、上的动点，连接，求线段长度的最小值．

问题解决

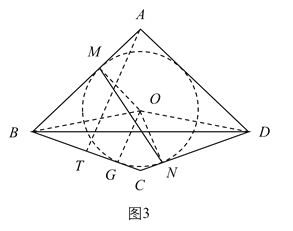
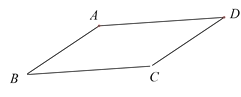
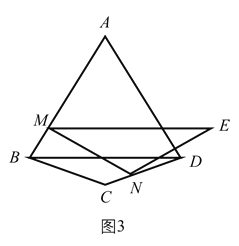
（3）如图（3），已知在四边形中，，，，连接，将线段沿方向平移至，点的对应点为点，点为边上一点，且，连接，的长度是否存在最小值？若存在，求出最小值；若不存在，请说明理由．

Answer 1

【答案】（1）2；（2）；（3）

【解析】

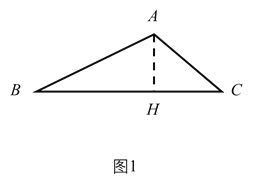
（1）如图1中，作AH⊥BC于H．设AH=CH=x，根据，构建方程即可解决问题．
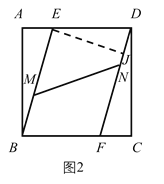
（2）如图2中，作EJ⊥DF于J．利用相似三角形的性质求出EJ，再根据垂线段最短即可解决问题．
（3）如图3中，如图3中，记MN的中垂线与AC的交点为点O，连接OM，ON，OB，OD，并以点O为圆心，OM为半径长作⊙O．以点O为圆心，OM为半径作圆，当⊙O与CD相切于 N时，即此时⊙O也与AB，BC相切，切点分别为M，G，此时MN最小．连接OG．设AC交BD于J，作AT⊥BC于T．利用相似三角形的性质求出MN即可．

解：（1）如图1中，作AH⊥BC于H．

在Rt△ACH中，∵∠C=45°，∠AHC=90°，
∴AH=CH，设AH=CH=x．
在Rt△ABH中，∵∠AHB=90°，∠B=30°，
∴BH=，
∴

∴x=2，即AH=2，
∴点A到BC的最短距离为2．

（2）如图2中，作EJ⊥DF于J，

∵四边形ABCD是正方形，
∴AB=BC=CD=AD=3，
∵，，
∴AE=CF=1，DE=BF=2，

∴DF=，
∵DE∥BF，
∴四边形BEDF是平行四边形，
∴BE∥DF，
∵EJ⊥DF，
∴∠EJD=∠EDC=∠C=90°，
∴∠EDJ＋∠CDF=90°，∠CDF＋∠CFD=90°，
∴∠EDJ=∠CFD，
∴△EDJ∽△DFC，

∴，

即

∴，

根据垂线段最短可知，MN的最小值为=；

（3）如图3中，记MN的中垂线与AC的交点为点O，连接OM，ON，OB，OD，并以点O为圆心，OM为半径长作⊙O．以点O为圆心，OM为半径作圆，当⊙O与CD相切于 N时，即此时⊙O也与AB，BC相切，切点分别为M，G，此时MN最小．连接OG．设AC交BD于J，作AT⊥BC于T．

在Rt△ABT中，∵∠ATB=90°，AB=3，∠ABT=60°，
∴BT=，AT=，

∴CT=BCBT=，

∴，

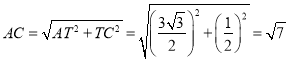∵AB=AD，CB=CD，
∴AC⊥BD，BJ=DJ，

∴
∴，
∵OM=OG，OM⊥AB，OG⊥BC，
∴OB平分∠ABC，
∴∠OBM=，
∴OB=2OM，
∵OB=OD，OM=ON，BM=DN，
∴△OMB≌△OND（SSS），
∴∠BOM=∠NOD，
∴∠MON=∠BOD，
∵OM=ON，OB=OD，
∴△MON∽△BOD，

∴，

∴，

∴MN的最小值为：．