题目内容
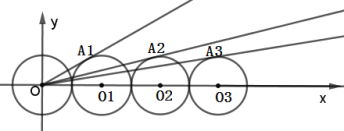
【题目】如图,在平面直角坐标中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
![]() ,
,![]() 的圆心在
的圆心在![]() 轴上,且半径均为
轴上,且半径均为![]() ,
,![]() 的坐标为
的坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]()
![]()
![]() 射线
射线![]() 与
与![]() 相切于点
相切于点![]() ,射线
,射线![]() 与
与![]() 相切于点
相切于点![]() ,按照这样的规律,
,按照这样的规律,![]() 的横坐标为_____.
的横坐标为_____.
【答案】![]()
【解析】
过点An作AnB⊥x轴于点B,连接AnOn,由切线的性质及所作的垂线可得∠OAnOn=∠AnBOn=90°,进而可证得△OOnAn∽△AnOnB,从而表示出OnB的长,再由![]() 计算即可.
计算即可.
解:如图,过点An作AnB⊥x轴于点B,连接AnOn,
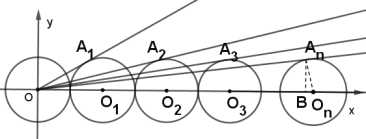
∵![]() 的坐标为
的坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]() ,
,![]() 坐标为
坐标为![]()
![]()
![]()
∴On的坐标为(2n,0)即OOn=2n,且AnOn=1,
∵射线![]() 与
与![]() 相切于点
相切于点![]() ,AnB⊥x轴,
,AnB⊥x轴,
∴∠OAnOn=∠AnBOn=90°,
又∵∠OOnAn=∠AnOnB
∴△OOnAn∽△AnOnB
∴![]()
∴![]()
∴![]()
∴![]()
故答案为:![]()

练习册系列答案
相关题目
【题目】某公司购进一批新产品进行销售,已知该产品的进货单价为8元/件,该公司对这批新产品上市后的销售情况进行了跟踪调查.销售过程中发现,该产品每月的销售量![]() (万件)与销售单价
(万件)与销售单价![]() (元)之间的关系满足下表.
(元)之间的关系满足下表.
销售单价 | … | 10 | 12 | 14 | 15 | … |
每月销售量 | … | 40 | 36 | 32 | 30 | … |
(1)请你从所学过的一次函数、二次函数和反比例函数三个模型中确定哪种函数能比较恰当地表示![]() 与
与![]() 的变化规律,并求出
的变化规律,并求出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)当销售单价为多少元时,该产品每月获得的利润为240万元?
(3)如果该产品每月的进货成本不超过160万元,那么当销售单价为多少元时,该产品每月获得的利润最大?最大利润为多少万元?