题目内容
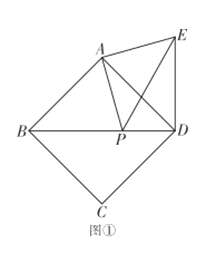
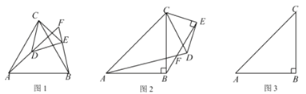
【题目】(1)如图1,△ABC和△CDE均为等边三角形,直线AD和直线BE交于点F.
①求证: AD=BE:
②求∠AFB的度数.
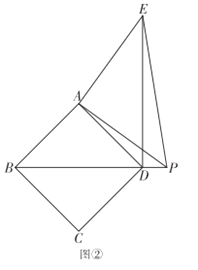
(2)如图2, △ABC和△CDE均为等腰直角三角形,∠ABC= ∠DEC=90°,直线AD和直线BE交于点F.
①求证: AD= ![]() BE:;
BE:;
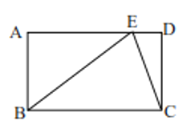
②若AB=BC=3, DE=EC= 2,将△CDE绕着点C在平面内旋转,当点D落在线段BC上时,在图3中画出图形,并求BF的长度.
【答案】(1)①见解析;②∠AFB=60°;(2)①见解析;②BF=![]() .
.
【解析】
(1)证明△ACD≌△BCE(SAS),即可解决问题.
(2)①根据∠ABC=∠DEC=90°,AB=BC,DE=EC,可知∠ACB=∠DCE=45°,∠ACD=∠BCE,可证△ACD∽△BCE,可知,![]()
②当点D落在线段BC上时,证明△ACD∽△BCE.再证明△BDF∽△BEC,可得![]() ,
,
即可计算出![]() .
.
(1)①∵△ABC和△CDE均为等边三角形,
∴CA=CB,CD=CE,∠ACB=∠DCE=60°.
∴∠ACD=∠BCE.
∴△ACD≌△BCE(SAS).
∴AD=BE,∠CAD=∠CBF.
②如图(1)设BC交AF于点G.
∵∠AGC=∠BGF,∠CAD=∠CBF,
∴∠BFG=∠ACG=60°.
即∠AFB=60°.
(2)①∵∠ABC=∠DEC=90°,AB=BC,DE=EC,
∴∠ACB=∠DCE=45°,![]() .
.
∴∠ACD=∠BCE.
∵![]()
∴△ACD∽△BCE.
∴![]() .
.
∴![]() .
.
②当点D落在线段BC上时,
如图所示
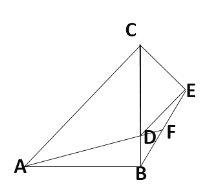
则![]() ,
,![]() .
.
过点E作EH⊥BC于点H,
则![]() ,
,![]() .
.
∴![]() .
.
∵∠ACD=∠BCE=45°,![]() .
.
∴△ACD∽△BCE.
∴∠CAD=∠CBE.
又∵∠ADC=∠BDF,
∴∠BFD=∠ACD=45°.
∴∠BFD=∠BCE=45°.
又∵∠DBF=∠EBC,
∴△BDF∽△BEC.
∴![]() .
.
∴![]() .
.
∴![]() .
.