题目内容
如图:直线y=ax+b分别与x轴,y轴相交于A、B两点,与双曲线y=
,(x>0)相交于点P,PC⊥x轴于点C,点A的坐标为(-4,0),点B的坐标为(0,2),PC=3.
(1)求双曲线对应的函数关系式;
(2)若点Q在双曲线上,且QH⊥x轴于点H,△QCH与△AOB相似,请求出点Q的坐标.

| k |
| x |
(1)求双曲线对应的函数关系式;
(2)若点Q在双曲线上,且QH⊥x轴于点H,△QCH与△AOB相似,请求出点Q的坐标.

(1)∵点A的坐标为(-4,0),点B的坐标为(0,2),
设y1=kx+b,
∴
,
解得:
,
故直线AB解析式为:y1=
x+2,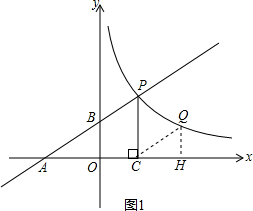
∵PC⊥x轴,PC=3,
∴3=
x+2,
解得:x=2,
故P(2,3),
则3=
,
解得k=6,
故双曲线的解析式为:y=
;
(2)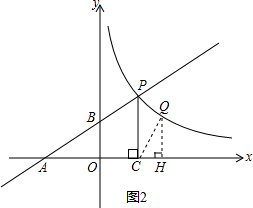 根据Q点在双曲线上,设Q点的坐标为(m,
根据Q点在双曲线上,设Q点的坐标为(m,
),
由A,B点的坐标可得:BO=2,AO=4,CO=2,
当△QCH∽△BAO时,
=
,
=
,
解得:m1=1+
,m2=1-
<0(不合题意舍去),
则
=
=
,
故Q点的坐标为:(
+1,
);
当△QCH∽△ABO时,
=
,
=
,
解得:m1=-1<0(不合题意舍去),m2=3,
则
=
=2,
故Q点的坐标为:(3,2).
综上所述:Q点的坐标为:(
+1,
);(3,2).
设y1=kx+b,
∴
|
解得:
|
故直线AB解析式为:y1=
| 1 |
| 2 |

∵PC⊥x轴,PC=3,
∴3=
| 1 |
| 2 |
解得:x=2,
故P(2,3),
则3=
| K |
| 2 |
解得k=6,
故双曲线的解析式为:y=
| 6 |
| x |
(2)
 根据Q点在双曲线上,设Q点的坐标为(m,
根据Q点在双曲线上,设Q点的坐标为(m,| 6 |
| m |
由A,B点的坐标可得:BO=2,AO=4,CO=2,
当△QCH∽△BAO时,
| QH |
| BO |
| CH |
| AO |
| ||
| 2 |
| m-2 |
| 4 |
解得:m1=1+
| 13 |
| 13 |
则
| 6 |
| m |
| 6 | ||
1+
|
| ||
| 2 |
故Q点的坐标为:(
| 13 |
| ||
| 2 |
当△QCH∽△ABO时,
| CH |
| BO |
| QH |
| AO |
| m-2 |
| 2 |
| ||
| 4 |
解得:m1=-1<0(不合题意舍去),m2=3,
则
| 6 |
| m |
| 6 |
| 3 |
故Q点的坐标为:(3,2).
综上所述:Q点的坐标为:(
| 13 |
| ||
| 2 |

练习册系列答案
相关题目