题目内容
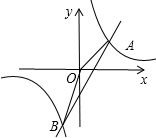
如图,已知反比例函数y=
的图象经过第二象限内的点A(-1,m),AB⊥x轴于点B,△AOB的面积为2.若直线y=ax+b经过点A,并且经过反比例函数y=
的图象上另一点C(n,一2).
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长;
(3)在双曲线上是否存在点P,使得△MBP的面积为8?若存在请求P点坐标;若不存在请说明理由.

| k |
| x |
| k |
| x |
(1)求直线y=ax+b的解析式;
(2)设直线y=ax+b与x轴交于点M,求AM的长;
(3)在双曲线上是否存在点P,使得△MBP的面积为8?若存在请求P点坐标;若不存在请说明理由.

(1)∵△AOB的面积为2,
∴
=2,
又∵函数图象在二、四象限,
∴k<0,
∴k=-4,
故y=-
,
则点A的坐标为(-1,4),点C的坐标为(2,-2),
将点A(-1,4),点C(2,-2),代入y=ax+b可得
,
解得:
,
故直线y=ax+b的解析式为:y=-2x+2;
(2)令y=0,可得x=1,
则点M的坐标为(1,0),
在Rt△ABM中,AB=4,BM=2,
则AM=
=2
;
(3)存在.
设点P的纵坐标为y,
则
BM×|y|=8,
解得:y=±8,
故点P的坐标为(-
,8)或(
,-8).
∴
| |k| |
| 2 |
又∵函数图象在二、四象限,
∴k<0,
∴k=-4,
故y=-
| 4 |
| x |
则点A的坐标为(-1,4),点C的坐标为(2,-2),
将点A(-1,4),点C(2,-2),代入y=ax+b可得
|
解得:
|
故直线y=ax+b的解析式为:y=-2x+2;
(2)令y=0,可得x=1,
则点M的坐标为(1,0),
在Rt△ABM中,AB=4,BM=2,
则AM=
| AB2+BM2 |
| 5 |
(3)存在.
设点P的纵坐标为y,
则
| 1 |
| 2 |
解得:y=±8,
故点P的坐标为(-
| 1 |
| 2 |
| 1 |
| 2 |

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目