题目内容
【题目】阅读下列材料：
材料一：最大公约数是指两个或多个整数共有的约数中最大的一个．我们将两个整数a、b的最大公约数表示为(a，b)，如(12，18)=6；(7，9)=1．
材料二：求7x+3y=11的一组整数解，主要分为三个步骤：
第一步，用x表示y，得y
；
第二步，找一个整数x，使得11﹣7x是3的倍数，为更容易找到这样的x，将11﹣7x变形为12﹣9x+2x﹣1=3(4﹣3x)+2x﹣1，即只需2x﹣1是3的倍数即可，为此可取x=2；
第三步，将x=2代入y，得y=﹣1．∴
是原方程的一组整数解．
材料三：若关于x，y的二元一次方程ax+by=c(a，b，c均为整数)有整数解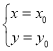
，则它的所有整数解为
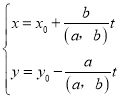(t为整数)．
利用以上材料，解决下列问题：
（1）求方程(15，20)x+(4，8)y=99的一组整数解；
（2）求方程(15，20)x+(4，8)y=99有几组正整数解．
【答案】（1）
；（2）原方程有5组正整数解．
【解析】
（1）先化简原方程，由材料可求解； （2）先求出原方程的整数解，根据材料即可求解．
（1）∵(15，20)=5，(4，8)=4，
∴原方程变形为：5x+4y=99，
∴x
，
∴99﹣4y是5的倍数，
∴当y=1时，x=19，
∴是原方程的解；
（2）∵5x+4y=99的有正整数解，
方程所有整数解为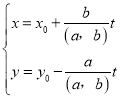
(t为整数)．
其中
方程所有正整数解记为
(t为整数)．
当
时，正整数解为：
，
当
时，正整数解为：
，
当
时，正整数解为：
，
当
时，正整数解为：
，
∴原方程有5组正整数解．
练习册系列答案
相关题目
