Question

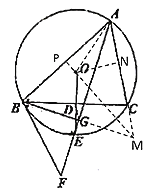
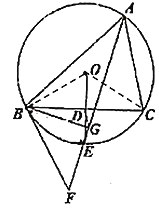
【题目】如图，点E为△ABC的外接圆⊙O上一点，OE⊥BC于点D，连接AE并延长至点F，使∠FBC＝∠BAC，

（1）求证：直线BF是⊙O的切线；

（2）若点D为OE中点，过点B作BG⊥AF于点G，连接DG，⊙O的半径为,AC=5.

①求∠BAC的度数；

②求线段DG的长.

Answer 1

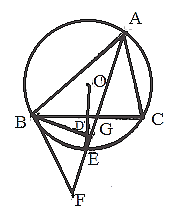
【答案】（1）详见解析；（2）①60°；②1.

【解析】

（1）连接OB、OC，由垂径定理、圆周角定理得∠BOD=∠BAC=∠FBC，根据∠BOD+∠OBD=90，得到∠FBC+∠OBD=90，即可证得直线BF是⊙O的切线；

（2）①由点D为OE中点，得到,利用cos∠BOD=，即可求出∠BOD=60，得到∠BAC=60；

②延长AC、BG交于点M，证明△ABM是等边三角形，由点D是BC的中点，G是BM的中点，得到DG是△BCM的中位线，过点M作MP⊥AB，过点O作ON⊥AM，连接OA，利用勾股定理求出ON的长，再利用勾股定理求出MN的长，即可求出MC的长度得到DG的长.

（1）连接OB、OC，

∵OE⊥BC，

∴∠BOD=∠BOC,∠ODB=90，

∵∠BAC=∠BOC,

∴∠BOD=∠BAC,

∵∠FBC＝∠BAC,∠BOD+∠OBD=90，

∴∠FBC+∠OBD=90，

即∠OBF=90，

∴OB⊥BF,

∴直线BF是⊙O的切线；

（2）①∵点D为OE中点，

∴,

∴cos∠BOD=，

∴∠BOD=60，

∴∠BAC=60；

②延长AC、BG交于点M，

∵OE⊥BC，

∴,BD=CD,

∵BG⊥AF，

∴∠AGB=90，

∴∠ABG=60,

∴△ABM是等边三角形，BG=AG,

∴DG是△BCM的中位线，

∴DG=CM,

过点M作MP⊥AB，

∴点P为AB的中点，∠AMP=30，

∴MP过点O,

过点O作ON⊥AM，连接OA，

∴AN=NC=AC=,

∵AO=,

∴,

∴，

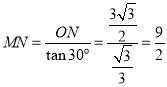∴MC=MN-NC=2，

∴DG=MC=1.