题目内容
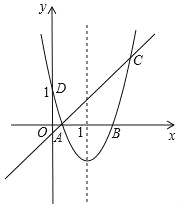
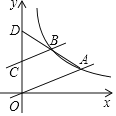
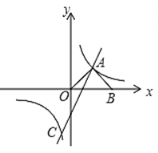
【题目】如图,在平面直角坐标系中,直线![]() 与双曲线
与双曲线![]() 交于A、C两点,
交于A、C两点,![]() 交x轴于点B,且OA=AB.
交x轴于点B,且OA=AB.
(1)求双曲线的解析式;
(2)求点C的坐标,并直接写出![]() 时x的取值范围;
时x的取值范围;
(3)设AC直线与y轴交于点D,求D点到OA的距离.
【答案】(1)![]() ;(2)C(-1,-4);
;(2)C(-1,-4);![]() 或
或![]() ;(3)
;(3)![]() 点到
点到![]() 的距离为
的距离为![]() .
.
【解析】
(1)作高线![]() ,根据等腰直角三角形的性质和点
,根据等腰直角三角形的性质和点![]() 的坐标的特点得:
的坐标的特点得:![]() ,可得
,可得![]() 的坐标,从而得双曲线的解析式;
的坐标,从而得双曲线的解析式;
(2)一次函数和反比例函数解析式列方程组,解出可得点![]() 的坐标,根据图象可得结论;
的坐标,根据图象可得结论;
(3)过点![]() 作
作![]() 于
于![]() ,由
,由![]() 点的坐标得出直线
点的坐标得出直线![]() 是
是![]() ,即可得出
,即可得出![]() 是等腰直角三角形,然后根据勾股定理即可求得.
是等腰直角三角形,然后根据勾股定理即可求得.
解:(1)∵点![]() 在直线
在直线![]() 上,
上,
∴设![]() ,
,
过![]() 作
作![]() 于
于![]() ,
,
∵![]() ,且
,且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
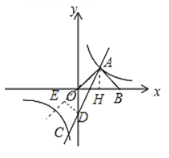
(2)∵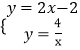 ,解得:
,解得: ![]() ,
, ![]() ,
,
∴![]() ,
,
由图象得:![]() 时
时![]() 的取值范围是
的取值范围是![]() 或
或![]() ;
;
(3)过点![]() 作
作![]() 于
于![]() ,
,
∵![]() ,
,
∴直线![]() 为:
为:![]() ,
,
∴![]() ,
,
∴![]() 是等腰直角三角形,
是等腰直角三角形,
由直线![]() 可知
可知![]() ,
,
∴![]() ,
,
∵![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() 点到
点到![]() 的距离为
的距离为![]() .
.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案【题目】某校为了了解全校400名学生参加课外锻炼的情况,随机对40名学生一周内平均每天参加课外锻炼的时间进行了调查,结果如下:(单位:分)
40 21 35 24 40 38 23 52 35 62 36 15 51 45 40 42 40 32 43 36
34 53 38 40 39 32 45 40 50 45 40 40 26 45 40 45 35 40 42 45
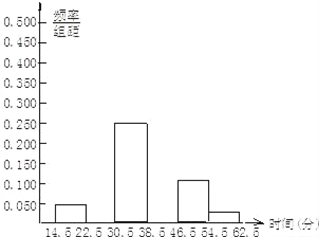
(1)补全频率分布表和频率分布直方图.
分组 | 频数 | 频率 |
4.5﹣22.5 | 2 | 0.050 |
22.5﹣30.5 | 3 | |
30.5﹣38.5 | 10 | 0.250 |
38.5﹣46.5 | 19 | |
46.5﹣54.5 | 5 | 0.125 |
54.5﹣62.5 | 1 | 0.025 |
合计 | 40 | 1.000 |
(2)填空:在这个问题中,总体是____,样本是____.由统计结果分析的,这组数据的平均数是38.35(分),众数是____,中位数是_____.
(3)如果描述该校400名学生一周内平均每天参加课外锻炼时间的总体情况,你认为用平均数、众数、中位数中的哪一个量比较合适?
(4)估计这所学校有多少名学生,平均每天参加课外锻炼的时间多于30分?