题目内容
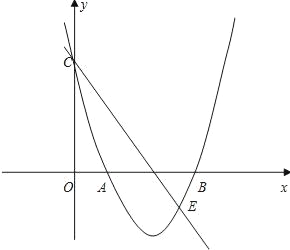
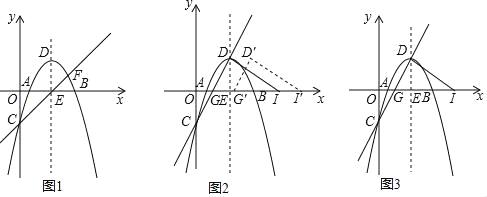
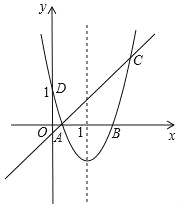
【题目】如图,一次函数y1=x﹣![]() 与x轴交点A恰好是二次函数y2与x轴的其中一个交点,已知二次函数图象的对称轴为x=1,并与y轴的交点为D(0,1).
与x轴交点A恰好是二次函数y2与x轴的其中一个交点,已知二次函数图象的对称轴为x=1,并与y轴的交点为D(0,1).
(1)求二次函数的解析式;
(2)设该二次函数与一次函数的另一个交点为C点,连接DC,求三角形ADC的面积.
(3)根据图象,直接写出当y1>y2时x的取值范围.
【答案】(1)y=![]() x2﹣
x2﹣![]() x+1;(2)S△ADC=
x+1;(2)S△ADC=![]() ;(3)
;(3)![]() <x<
<x<![]() .
.
【解析】
(1)根据题意求得A点坐标,用待定系数法求解即可.
(2)根据题意求得C,D两点的坐标,进而求得三角形的面积.
(3)观察图像即可得到y1>y2时x的取值范围.
解:(1)由已知可得y=x﹣![]() 与x轴交点A的坐标为(
与x轴交点A的坐标为(![]() ,0)
,0)
∵二次函数过(0,1)
∴设二次函数的解析式为y=ax2+bx+1
∵二次函数图象的对称轴为x=1,且过A(![]() ,0)
,0)
∴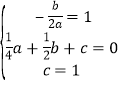 ,解得
,解得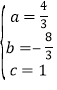
∴二次函数的解析式为:y=![]() x2﹣
x2﹣![]() x+1;
x+1;
(2)由(1)知函数y=![]() x2﹣
x2﹣![]() x+1过A(
x+1过A(![]() ,0),
,0),
当y=0时,0=![]() x2﹣
x2﹣![]() x+1,解得x1=
x+1,解得x1=![]() ,x2=
,x2=![]() ,
,
∴B(![]() ,0)
,0)
解方程组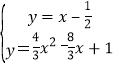 得
得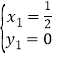 或
或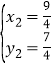 ,则C(
,则C(![]() ,
,![]() )
)
直线y=x﹣![]() 与y轴的交点坐标为(0,﹣
与y轴的交点坐标为(0,﹣![]() ),
),
∴S△ADC=![]() ×(1+
×(1+![]() )(
)(![]() ﹣﹣
﹣﹣![]() )=
)=![]() ;
;
(3)根据图象知,当y1>y2时,x的取值范围是![]() <x<
<x<![]() .
.

练习册系列答案
相关题目