Question

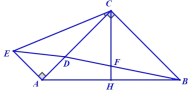
【题目】如图Rt△ABC中∠BAC=90°，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得△AFB，连接EF，下列结论：①△AED≌△AEF；②△ABC的面积等于四边形AFBD的面积；③BE+DC=DE；④BE2+DC2=DE2；⑤∠DAC=22.5°，其中正确的是（　　）

A. ①②④B. ③④⑤C. ①③④D. ①②⑤

Answer 1

【答案】A

【解析】

①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；
②根据旋转的性质，△ADC≌△ABF，进而得出△ABC的面积等于四边形AFBD的面积；
③根据①知道△ADE≌△AFE，得CD=BF，DE=EF；由此即可确定说法是否正确；
④据①BF=CD，EF=DE，∠FBE=90°，根据勾股定理判断．
⑤可以利用①②④正确，利用答案中没有更多正确答案，得出⑤错误．

①根据旋转的性质知∠CAD=∠BAF，AD=AF，

∵

∴

∴

∴△AEF≌△AED；

故①正确；

②∵根据旋转的性质,∴△ADC≌△AFB，

∴△ABC的面积等于四边形AFBD的面积；

故此选项正确；

③根据①知道△ADE≌△AFE，得CD=BF，DE=EF，

∴BE+DC=BE+BF>DE=EF，

故③错误；

④∵AB=AC,△ADC旋转至△AFB，

∴

根据旋转的性质可得△ADC≌△AFB,

∴

∴

∵△ADC绕点A顺时针旋转后，得到△AFB，

∴△AFB≌△ADC，

∴BF=CD，

又∵EF=DE，

∴ 故④正确.

⑤∵可以利用①②④正确，利用答案中没有更多正确答案，得出⑤错误.

故正确的有：①②④.

故选:A.