Question

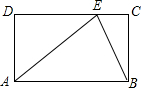
如图：在矩形ABCD中，对角线AC、BD交于点O，AB=8cm，AD=10cm，PE⊥AC，垂足为E，PF⊥BD垂足为F，求PE+PF．

Answer 1

连接OP，
∵四边形ABCD是矩形，
∴∠BAD=90°，AC=BD，AO=OC，OD=OB，
∴OA=OD=OC=OB，
在Rt△BAD中，由勾股定理得：AC=BD=

82+102

=2

41

（cm），
∴OA=OD=

41

cm，
∵S_△DPO+S_△APO=S_△AOD=

1

2

S_△ABD，
∴

1

2

OA×PE+

1

2

OD×PF=

1

2

×

1

2

AD×AB，
∴

41

PE+

41

PF=

1

2

×8×10，
∴PE+PF=

40 41

41

（cm）．