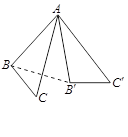
题目内容
如图,Rt 绕O点逆时针旋转
绕O点逆时针旋转 得Rt
得Rt ,其中∠ABD=∠ACB=∠BED=
,其中∠ABD=∠ACB=∠BED= ,AC=3,DE=5,则OC的长为( )
,AC=3,DE=5,则OC的长为( )
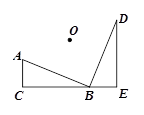
 绕O点逆时针旋转
绕O点逆时针旋转 得Rt
得Rt ,其中∠ABD=∠ACB=∠BED=
,其中∠ABD=∠ACB=∠BED= ,AC=3,DE=5,则OC的长为( )
,AC=3,DE=5,则OC的长为( )
A. | B. | C.3+2 | D.4+ |
B
Rt△ABC绕O点旋转90°得Rt△BDE,C、E两点为对应点,由旋转的性质可知,OC=OE,∠COE=90°,AC与BE,BC与DE对应,故有CE=BE+BC=AC+DE=8,再由勾股定理求OC.

解:连接OC、OE.
由旋转的性质可知,OC=OE,∠COE=90°,
∵AC与BE,BC与DE对应,
∴CE=BE+BC=AC+DE=8,
∴由勾股定理得,OC2+OE2=CE2,
即2OC2=64,解得OC=4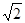 .
.
故选B.
本题考查了旋转的基本性质:旋转图形全等,对应点到旋转中心的距离相等,对应点与旋转中心连线的夹角为旋转角,同时,考查了勾股定理的运用.

解:连接OC、OE.
由旋转的性质可知,OC=OE,∠COE=90°,
∵AC与BE,BC与DE对应,
∴CE=BE+BC=AC+DE=8,
∴由勾股定理得,OC2+OE2=CE2,
即2OC2=64,解得OC=4
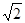 .
.故选B.
本题考查了旋转的基本性质:旋转图形全等,对应点到旋转中心的距离相等,对应点与旋转中心连线的夹角为旋转角,同时,考查了勾股定理的运用.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
 绕点
绕点 顺时针旋转150°后得到△
顺时针旋转150°后得到△ ,连结
,连结 .若
.若 . 则△
. 则△ 的面积为 .
的面积为 .

 在
在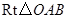 中,
中,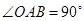 ,且点
,且点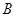 的坐标为(4,2).
的坐标为(4,2).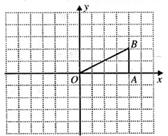
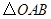 绕点
绕点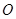 逆时针旋转
逆时针旋转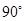 后的
后的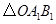 ;
; 旋转到点
旋转到点 所经过的路线长.
所经过的路线长.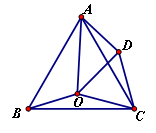
 以点
以点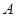 为旋转中心,按逆时针方向旋转
为旋转中心,按逆时针方向旋转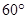 ,得
,得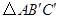 ,则
,则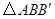 是 三角形。
是 三角形。