题目内容
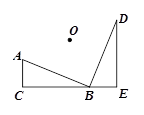
如图所示，将含30°角的直角三角尺
绕点
顺时针旋转150°后得到△
，连结
.若
. 则△
的面积为 ．
绕点顺时针旋转150°后得到△，连结.若. 则△的面积为 ．
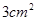
解：过D点作BE的垂线，垂足为F，
∵∠ABC=30°，∠ABE=150°
∴∠CBE=∠ABC+∠ABE=180°，
∵在Rt△ABC中，AB=4，∠ABC=30°，
∴AC=2，BC=2
，
由旋转的性质可知BD=BC=2，DE=AC=2，BE=AB=4，
由DF×BE=BD×DE，即DF×4=2×2，
解得DF=，
S△BCD=
×BC×DF=×2×=3cm2．．
故答案为：3cm2．
∵∠ABC=30°，∠ABE=150°
∴∠CBE=∠ABC+∠ABE=180°，
∵在Rt△ABC中，AB=4，∠ABC=30°，
∴AC=2，BC=2
，由旋转的性质可知BD=BC=2
，DE=AC=2，BE=AB=4，由DF×BE=BD×DE，即DF×4=2
×2，解得DF=
，S△BCD=
×BC×DF=×2×=3cm2．．故答案为：3cm2．
练习册系列答案
相关题目
的方向滚动， 直至△MNP中有一个点与点B重合为止，则点P经过的路程为 ；（2）如图二，正方形MNPQ的边长为1，正方形ABCD的边长为2，点M与点A重合，点N在线段AB上， 点P在正方形内部，正方形MNPQ沿正方形ABCD的边按
的方向滚动，始终保持M,N,P,Q四点在正方形内部或边界上，直至正方形MNPQ回到初始位置为止， 则点P经过的最短路程为 .
，则点
绕O点逆时针旋转
得Rt
，其中∠ABD=∠ACB=∠BED=
