Question

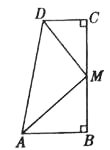
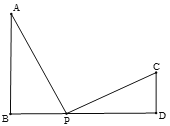
【题目】如图，已知AB⊥BD，CD⊥BD点P是BD上一点.

（1）若∠APC=90°.求证：△PAB∽△CPD；

（2）若△PAB与△PCD相似，AB=9，BP=6，CD=4.求PD的长．

Answer 1

【答案】（1）证明见解析；（2）或6.

【解析】

（1）由于AB⊥BD，CD⊥BD，可知∠B与∠D为直角，又∠APC=90°，则∠APB+∠CPD=90°，可以得出∠A=∠CPD，从而证出△ABP∽△PDC．

（2）分两种情况讨论：①若 △∽△ △∽△，据此，即可利用相似三角形的性质列出比例式，从而求出线段PD的值．

（1）证明：∵，

∴90°

∵°

∴°

∵在△中 °

∴

在△和△中

∴△∽△

（2）解： ①若 △∽△，则

∴ 解得

②若 △∽△，则

∴ 解得

综上所述，的长为或6.