题目内容
【题目】已知:如图,AB是⊙O的弦,⊙O的半径为10,OE、OF分别交AB于点E、F,OF的延长线交⊙O于点D,且AE=BF,∠EOF=60°.
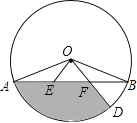
(1)求证:△OEF是等边三角形;
(2)当AE=OE时,求阴影部分的面积.(结果保留根号和π)
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)作OC⊥AB于点C,由OC⊥AB可知AC=BC,再根据AE=BF可知EC=FC,因为OC⊥EF,所以OE=OF,再由∠EOF=60°即可得出结论.
(2)在等边△OEF中,因为∠OEF=∠EOF=60°,AE=OE,所以∠A=∠AOE=30°,故∠AOF=90°,再由AO=10可求出OF的长,根据S阴影=S扇形AOD﹣S△AOF即可得出结论.
解:(1)证明:作OC⊥AB于点C,
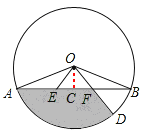
∵OC⊥AB,∴AC=BC.
∵AE=BF,∴EC=FC.
∵OC⊥EF,∴OE=OF.
∵∠EOF=60°,∴△OEF是等边三角形.;
(2)∵在等边△OEF中,∠OEF=∠EOF=60°,AE=OE,
∴∠A=∠AOE=30°.∴∠AOF=90°.
∵AO=10,∴OF=![]() .
.
∴![]() ,
,![]() .
.
∴![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】下表是某班体育考试跳绳项目模拟考试时10名同学的测试成绩(单位:个/分钟)
成绩(个/分钟) | 140 | 160 | 169 | 170 | 177 | 180 |
人数 | 1 | 1 | 1 | 2 | 3 | 2 |
则关于这10名同学每分钟跳绳的测试成绩,下列说法错误的是( )
A.方差是135B.平均数是170C.中位数是173.5D.众数是177