题目内容
【题目】已知:如图,四边形ABED是正方形,DB⊥BC,点E为线段DC的中点,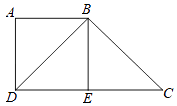
(1)求证:BD2=ADDC.
(2)连接AE,求证:ABCE为平行四边形.
【答案】
(1)解:证明:∵四边形ABED是正方形,
∴∠A=90°,AB=AD,∠ADB=∠ABD=45°,
∵BE⊥CD,点E为线段DC的中点,
∴BD=BC,
∵DB⊥BC,
∴∠BDC=∠C=45°,
∴△ABD∽△DBC,
∴ ![]() ,
,
∴BD2=ADDC;
(2)解:证明:连接AE,
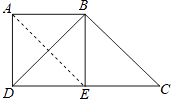
∵四边形ABED是正方形,
∴∠AED=45°,AB∥CD,
∵∠C=45°,
∴∠AED=∠C,
∴AE∥BC,
∴四边形ABCE为平行四边形.
【解析】(1) 由正方形的性质知∠A=90°,AB=AD,∠ADB=∠ABD=45°又由中垂线的性质知BD=BC,进而得出△ABD∽△DBC,由相似三角形对应边成比例得出结论;由正方形的性质得出∠AED=45°,AB∥CD,进而得出∠AED=∠C,故AE∥BC,从而四边形ABCE为平行四边形.
【考点精析】解答此题的关键在于理解平行四边形的判定的相关知识,掌握两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

练习册系列答案
 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案
相关题目





