Question

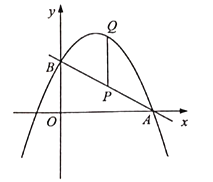
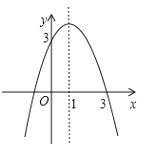
【题目】已知，二次函数的图象，如图所示，解决下列问题：

（1）关于的一元二次方程的解为；

（2）求出抛物线的解析式；

（3）为何值时．

Answer 1

【答案】（1）-1或3；（2）抛物线解析式为y=-x2+2x+3；（3）x＞3或x＜-1．

【解析】

（1）直接观察图象，抛物线与x轴交于-1，3两点，所以方程的解为x1=-1，x2=3．
（2）设出抛物线的顶点坐标形式，代入坐标（3，0），即可求得抛物线的解析式．
（3）若y＜0，则函数的图象在x轴的下方，找到对应的自变量取值范围即可．

解：（1）观察图象可看对称轴出抛物线与x轴交于x=-1和x=3两点，
∴方程的解为x1=-1，x2=3，
故答案为：-1或3；
（2）设抛物线解析式为y=-（x-1）2+k，
∵抛物线与x轴交于点（3，0），
∴（3-1）2+k=0，
解得：k=4，
∴抛物线解析式为y=-（x-1）2+4，
即：抛物线解析式为y=-x2+2x+3；
（3）抛物线与x轴的交点（-1,0），（3,0），当y＜0时，则函数的图象在x轴的下方，由函数的图象可知：x＞3或x＜-1；