题目内容
【题目】如图,已知在平面直角坐标系xOy中,抛物线![]() 经过原点,且与
经过原点,且与![]() 轴相交于点
轴相交于点![]() ,点
,点![]() 的横坐标为6,抛物线顶点为点
的横坐标为6,抛物线顶点为点![]() .
.
(1)求这条抛物线的表达式和顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() ,在直线
,在直线![]() 上点取一点
上点取一点![]() ,使得
,使得![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将该抛物线向左平移![]() 个单位,所得新抛物线与
个单位,所得新抛物线与![]() 轴负半轴相交于点
轴负半轴相交于点![]() 且顶点仍然在第四象限,此时点
且顶点仍然在第四象限,此时点![]() 移动到点
移动到点![]() 的位置,
的位置,![]() ,求
,求![]() 的值.
的值.
【答案】(1)![]()
![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将点O,点A坐标代入解析式可求抛物线的表达式和顶点B的坐标;
(2)由点A,点B坐标可求直线AB解析式,即可求直线OP解析式为:y=![]() x,设点Q(3k,4k),可证四边形OQAP为等腰梯形,可得OB=QA,由两点距离公式可求k的值,即可求点Q坐标;
x,设点Q(3k,4k),可证四边形OQAP为等腰梯形,可得OB=QA,由两点距离公式可求k的值,即可求点Q坐标;
(3)过点B分别做作x、y轴垂线,垂足分别为点E、F,由题意可证△BCF∽△BDE,可得![]() ,可得
,可得![]() ,可得
,可得![]() ,可得关于m的方程,即可求m的值.
,可得关于m的方程,即可求m的值.
(1)∵点![]() 、
、![]() 在抛物线
在抛物线![]() 上
上
∴ ,解得
,解得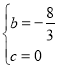
∴抛物线的解析式为![]() ,
,
∴顶点B的坐标是![]() ;
;
(2)如图,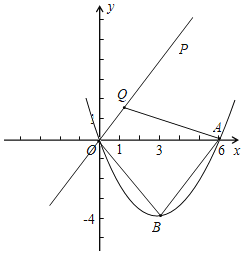
∵![]() ,
,![]()
∴直线AB解析式为:y=![]() x-8,
x-8,
∵![]()
∴直线OP解析式为:y=![]() x,
x,
设点![]() ,
,
∵∠OBA=∠QAB>∠OAB,
∴k>0
∵OP平于AB,QA不平行于OB
∴四边形OQAB为梯形
又∵∠QAB=∠OBA
∴四边形OQAB为等腰梯形
∴QA=OB
∴(6-3k)2+(4k)2=25
∴![]() 或
或![]() (舍去)
(舍去)
∴![]()
(3)由(1)知![]()
设抛物线向左平移![]() 个单位后的新抛物线表达式为
个单位后的新抛物线表达式为![]()
∵新抛物线与y轴负半轴相交于点C且顶点仍然在第四象限,设点C的坐标为C(0,c)
∴0<m<3,-4<c<0,
如图,过点B分别做作x、y轴垂线,垂足分别为点E、F
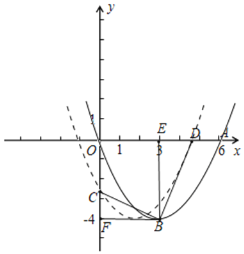
∴![]() 且
且![]()
∴![]() ∽
∽![]()
∴![]()
∴![]()
∴![]()
∴ ![]()
又∵![]()
∴ ![]()
∴ ![]()
∴![]() 或者
或者![]() (舍去)
(舍去)
∴ ![]()

练习册系列答案
相关题目