题目内容
【题目】如图,点A(![]() ,4),B(3,m)是直线AB与反比例函数
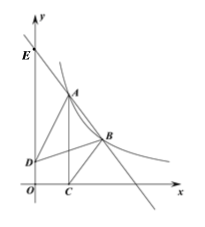
,4),B(3,m)是直线AB与反比例函数![]() (x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
(x>0)图象的两个交点.AC⊥x轴,垂足为点C,已知D(0,1),连接AD,BD,BC.
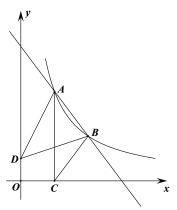
(1)求直线AB的表达式;
(2)△ABC和△ABD的面积分别为S1,S2,求S2-S1.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)先由A点坐标求出反比例函数的表达式,再求出B点坐标,最后运用待定系数法求直线AB的表达式即可;
(2)![]() 的面积可由“底乘高除以2”直接求得,
的面积可由“底乘高除以2”直接求得,![]() 的面积运用“补”的思想求出,然后两者作差即可得.
的面积运用“补”的思想求出,然后两者作差即可得.
(1)由点![]() 在反比例函数
在反比例函数![]() 的图象上
的图象上
∴![]()
∴![]()
∴反比例函数的表达式为![]()
将点![]() 代入
代入![]() 得
得![]()
∴![]()
设直线AB的表达式为![]()
将点![]() 代入得
代入得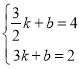 , 解得
, 解得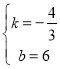
则直线AB的表达式为![]() ;
;
(2)由点A、B的坐标得![]() ,点B到AC的距离为
,点B到AC的距离为![]()
∴![]()
如图,设直线AB与y轴的交点为E
令![]() 得
得![]() ,则点E的坐标为
,则点E的坐标为![]()
![]()
∴![]()
由点![]() 得:点A、B到DE的距离分别为
得:点A、B到DE的距离分别为![]() ,3
,3
∴![]()
则![]() .
.

练习册系列答案
相关题目