题目内容
【题目】如图,在线段BC上有两点E,F,在线段CB的异侧有两点A,D,满足AB=CD,AE=DF,CE=BF,连接AF;
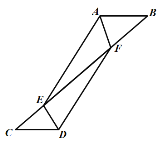
(1)连接DE,求证:四边形AEDF是平行四边形;
(2)若∠B=40°,∠DFC=30°,当AF平分∠BAE时,求∠BAF.
【答案】(1)见解析 (2)55°
【解析】
(1)先证明△ABE≌△DCF,进而证得AE∥DF,再结合AE=DF即可证明;
(2)由△ABE≌△DCF,可得∠AEB=∠DFC=30°,然后由三角形内角和定理可得∠BAE=110°,最后根据角平分线的性质解答即可.
(1)证明:∵CE=BF,
∴CE+EF=BF+EF,
∴BE=CF,
在△ABE和△DCF中,
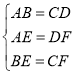 ,
,
∴△ABE≌△DCF(SSS),
∴∠BEA=∠CFD;
∴AE∥DF,
又∵AE=DF,
∴四边形AEDF是平行四边形
(2)解:由(1)得:△ABE≌△DCF,
∴∠AEB=∠DFC=30°,
∴∠BAE=180°﹣∠B﹣∠AEB=180°﹣40°﹣30°=110°,
∵AF平分∠BAE,
∴∠BAF=![]() ∠BAE=
∠BAE=![]() ×110°=55°
×110°=55°

练习册系列答案
相关题目