Question

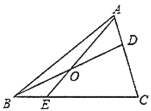
【题目】有这样一个问题，如图1，在等边中，，为的中点，，分别是边，上的动点，且，若，试求的长．爱钻研的小峰同学发现，可以通过几何与函数相结合的方法来解决这个问题，下面是他的探究思路，请帮他补充完整．

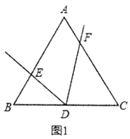
（1）注意到为等边三角形，且，可得，于是可证，进而可得，注意到为中点，，因此和满足的等量关系为______．

（2）设，，则的取值范围是______．结合（1）中的关系求与的函数关系．

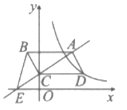
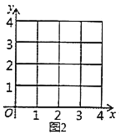
（3）在平面直角坐标系中，根据已有的经验画出与的函数图象，请在图2中完成画图．

（4）回到原问题，要使，即为，利用（3）中的图象，通过测量，可以得到原问题的近似解为______（精确到0.1）

Answer 1

【答案】（1）；（2），；（3）答案见解析；（4）1.6．

【解析】

（1）利用相似三角形的性质即可解决问题．
（2）求出当点F与点A重合时BE的值即可判断x的取值范围．
（3）利用描点法画出函数图象即可．
（4）画出两个函数图象，量出点P的横坐标即可解决问题．

解：（1）由，可得，

∵，

∴.

故答案为：

（2）由题意：．

∵由，可得，

∵，，．

∴，

∴．

故答案为：；.

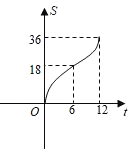
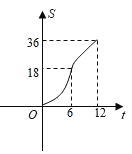
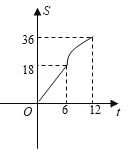
（3）函数图象如图所示：

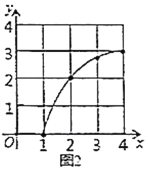
（4）观察图象可知两个函数的交点P的横坐标约为1.6，故BE=1.6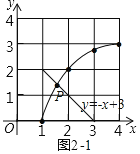

故答案为1.6．