Question

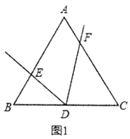
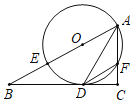
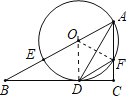
【题目】已知：△ABC中∠ACB＝90°，E在AB上，以AE为直径的⊙O与BC相切于D，与AC相交于F，连接AD．

（1）求证：AD平分∠BAC；

（2）若DF∥AB，则BD与CD有怎样的数量关系？并证明你的结论．

Answer 1

【答案】(1)见解析；(2) BD＝2CD证明见解析

【解析】

（1）连接OD．根据圆的半径都相等的性质及等边对等角的性质知：∠OAD＝∠ODA；再由切线的性质及平行线的判定与性质证明∠OAD＝∠CAD；

（2）连接OF，根据等腰三角形的性质以及圆周角定理证得∠BAC＝60°，根据平行线的性质得出BD：CD＝AF：CF，∠DFC＝∠BAC＝60°，根据解直角三角形即可求得结论．

（1）证明：连接OD，

∴OD＝OA，

∴∠OAD＝∠ODA，

∵BC为⊙O的切线，

∴∠ODB＝90°，

∵∠C＝90°，

∴∠ODB＝∠C，

∴OD∥AC，

∴∠CAD＝∠ODA，

∴∠OAD＝∠CAD，

∴AD平分∠BAC；

（2）连接OF，

∵DF∥AB，

∴∠OAD＝∠ADF，

∵AD平分∠BAC，

∴∠ADF＝∠OAF，

∵∠ADF＝∠AOF，

∴∠AOF＝∠OAF，

∵OA＝OF，

∴∠OAF＝∠OFA，

∴△AOF是等边三角形，

∴∠BAC＝60°，

∵∠ADF＝∠DAF，

∴DF＝AF，

∵DF∥AB，

∴BD：CD＝AF：CF，∠DFC＝∠BAC＝60°，

∴＝2，

∴BD＝2CD．