题目内容
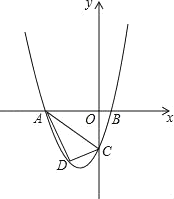
【题目】如图,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,点
两点,点![]() 在线段
在线段![]() 上(不含端点
上(不含端点![]() 、
、![]() ).
).

(1)求![]() 、
、![]() 两点的坐标;
两点的坐标;
(2)若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)若![]() 交直线
交直线![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 为
为![]() 中点,当点
中点,当点![]() 在线段
在线段![]() 上滑动时,求证
上滑动时,求证![]() 的值不变.
的值不变.
【答案】(1)A的坐标为(2,0)、B的坐标为(0,2);(2)C的坐标为(![]() );(3)证明过程见解析.
);(3)证明过程见解析.
【解析】
(1)在直线![]() 中分别令y=0,x=0可求得A、B两点的坐标;
中分别令y=0,x=0可求得A、B两点的坐标;
(2)根据面积比,可以求得C的横纵坐标比,由C在直线AB上,代入直线解析式即可得出答案;
(3)根据条件可证△DBO≌△FOA,可得BD=FO,从而可得到BD+BF=BO,可得出结论.
解:(1)∵直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点
两点
∴当x=0时,y=2;当y=0时,x=2
∴A的坐标为(2,0)、B的坐标为(0,2).
(2)∵![]()
∴![]()
又C在直线![]() 上
上
∴C的坐标为(![]() ).
).
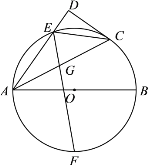
(3)∵BD∥OA,AE⊥OC
∴∠D=∠DOA
∵∠DOA+∠DOF=90°
∠AFO+∠DOF=90°
∴∠DOA=∠AFO
∴∠D=∠AFO
在△DBO和△FOA中
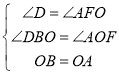
∴△DBO≌△FOA(AAS)
∴BD=FO
∴BD+BF=FO+BF=BO
∵BO=2
∴BD+BF=2
即BD+BF是定值不变.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目