题目内容
【题目】已知:如图,正方形ABCD,点E是DC边上的一动点,过点C作AE的垂线交AE延长线于点F,过D作DH⊥CF,垂足为H,点O是AC中点,连HO.
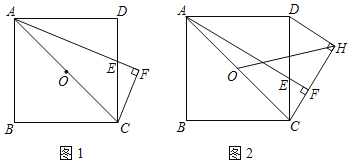
(1)如图1,当∠CAE=∠DAE时,证明:AE=2CF;
(2)如图2,当点E在DC上运动时,线段AF与线段HO之间是否存在确定的数量关系?若存在,证明你发现的结论:若不存在,请说明理由;
(3)当E为DC中点时,AC=2![]() ,直接写出AF的长 .
,直接写出AF的长 .
【答案】(1)证明见解析;(2)AF=![]() OH,理由见解析;(3)
OH,理由见解析;(3)![]() .
.
【解析】
(1)如图1,延长AD、CH交于M,证明△ACF≌△AMF(ASA),得CM=2CF,再证明△ADE≌△CDM(ASA),可得结论;
(2)如图2,作辅助线,构建全等三角形,证明△OMC≌△OND(AAS),并证明四边形MONH是正方形,得OH=![]() OM,根据三角形中位线定理可得是结论;
OM,根据三角形中位线定理可得是结论;
(3)如图1,证明△ADE∽△CFE,得CF=2EF,利用正方形的性质和勾股定理计算AD=CD=2,分别计算AE和EF的长可得结论.
(1)证明:如图1,延长AD、CH交于M,

∵AF⊥CF,
∴∠AFC=∠AFM=90°,
∵∠DAE=∠CAE,AF=AF,
∴△ACF≌△AMF(ASA),
∴CF=FM,
∴CM=2CF,
∵四边形ABCD是正方形,
∴AD=CD,∠ADC=90°,
∴∠ADC=∠CDM=90°,
∵∠ADE=∠EFC=90°,∠AED=∠CEF,
∴∠ECF=∠EAD,
∴△ADE≌△CDM(ASA),
∴AE=CM=2CF;
(2)解:AF=![]() OH,理由是:
OH,理由是:
如图2,过O作ON⊥DH于N,OM⊥CH于M,连接OD,

∴∠OMH=∠ONH=∠MHN=90°,
∴四边形MONH为矩形,
∴∠MON=90°,
∵四边形ABCD是正方形,
∴OD=OC,∠DOC=90°,
∴∠MOC=∠DON,
∵∠OMC=∠OND=90°,
∴△OMC≌△OND(AAS),
∴OM=ON,
∴矩形MONH是正方形,
∴OH=![]() OM,
OM,
△ACF中,∵OA=OC,OM∥AF,
∴CM=FM,
∴AF=2OM,
∴![]() =
=![]() ,即AF=
,即AF=![]() OH;
OH;
(3)∵∠ADE=∠EFC=90°,∠AED=∠CEF,
∴△ADE∽△CFE,
∴![]() =
=![]() =
=![]() =2,
=2,
∵四边形ABCD是正方形,且AC=2![]() ,
,
∴AD=CD=2,
∵E是CD的中点,
∴DE=CE=1,
由勾股定理得:AE=![]() =
=![]() =
=![]() ,
,
设EF=x,则CF=2x,
∴CE=![]() x=1,
x=1,
x=![]() ,
,
∴EF=![]() ,
,
∴AF=![]() +
+![]() =
=![]() .
.
故答案为:![]() .
.

 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案