题目内容
【题目】如图,![]() 为
为![]() 的直径,且
的直径,且![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,![]() ,,
,,![]() 于
于![]() ,
,![]() 为半圆弧
为半圆弧![]() 的中点,
的中点,![]() 交
交![]() 于点
于点![]() .
.
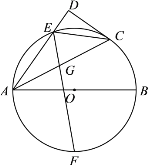
(1)求![]() 的长;
的长;
(2)求![]() 的长.
的长.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)连接EB,OC交于M,根据角平分线定义得到∠DAC=∠BAC,根据垂径定理得到OC⊥BE,推出四边形MCDE是矩形,根据勾股定理即可得到结论;
(2)过G作GR⊥AD于R,GS⊥BE于S,设![]() ,由F为半圆弧AB的中点,得到∠AEF=∠BEF,根据三角形的面积公式即可得到结论.
,由F为半圆弧AB的中点,得到∠AEF=∠BEF,根据三角形的面积公式即可得到结论.

解:(1)连接EB,OC交于M,
∵AC平分∠DAB交⊙O于点E,
∴∠DAC=∠BAC,
∴![]() ,
,
∴![]() ,
,![]()
∵AB为⊙O的直径,
∴BE⊥AD,
∵AD⊥CD于D,
∴四边形MCDE是矩形,
∵AE=6,AB=10,
∴![]() ;
;
(2)过G作GR⊥AD于R,GS⊥BE于S,设![]() ,
,
∵F为半圆弧AB的中点,
∴![]() ,
,
∴![]() ,
,
∵![]() 平分
平分![]() ,
,
∴G点为![]() 的内接圆心,
的内接圆心,
∵![]() ,
,
即是:![]() ,
,
∴![]() ,
,
∴在等腰直角![]() 中:
中:![]() .
.

练习册系列答案
相关题目
【题目】已知关于x的方程(x-3)(x-2)-p2=0.
(1)求证:无论p取何值时,方程总有两个不相等的实数根;
(2)设方程两实数根分别为x1、x2,且满足x12+x22=3 x1x2,求实数p的值.