题目内容
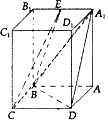
【题目】在四棱柱ABCD﹣A1B1C1D1中,四边形ABCD为平行四边形,AA1⊥平面ABCD,∠BAD=60°,AB=2,BC=1.AA1= ![]() ,E为A1B1的中点.
,E为A1B1的中点. 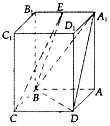
(1)求证:平面A1BD⊥平面A1AD;
(2)求多面体A1E﹣ABCD的体积.
【答案】
(1)证明:∵AB=2,AD=BC=1,∠BAD=60°,
∴BD= ![]() =
= ![]() ,
,
∴BD2+AD2=AB2,∴AB⊥AD,
∵AA1⊥平面ABCD,BD平面ABCD,
∴BD⊥AA1,又AA1∩AD=A,AA1平面A1AD,AD平面A1AD,
∴BD⊥平面A1AD,又BD平面A1BD,
∴平面A1BD⊥平面A1AD.
(2)解:连接A1C,S四边形ABCD=2S△ABD=2× ![]() =
= ![]() ,
,
∴V ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
设C到AB的距离为h,则h= ![]() =
= ![]() ,则C到平面ABB1A1的距离为h=
,则C到平面ABB1A1的距离为h= ![]() ,
,
∴V ![]() =
= ![]() =
= ![]() =
= ![]() .
.
∴多面体A1E﹣ABCD的体积V=V ![]() +V
+V ![]() =
= ![]() .
.
【解析】(1)求出BD,再利用勾股定理的逆定理证明BD⊥AD,结合BD⊥AA1即可得出BD⊥平面A1AD,从而平面A1BD⊥平面A1AD;(2)将多面体分解成三棱锥C﹣A1BE和四棱锥A1﹣ABCD,分别计算两个棱锥的体积即可得出多面体的体积.
【考点精析】认真审题,首先需要了解平面与平面垂直的判定(一个平面过另一个平面的垂线,则这两个平面垂直).

【题目】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]. 
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如表所示,求数学成绩在[50,90)之外的人数.
分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
x:y | 1:1 | 2:1 | 3:4 | 4:5 |
【题目】某厂家为了解销售轿车台数与广告宣传费之间的关系,得到如表统计数据表:根据数据表可得回归直线方程 ![]() ,其中
,其中 ![]() ,
, ![]() ,据此模型预测广告费用为9万元时,销售轿车台数为( )
,据此模型预测广告费用为9万元时,销售轿车台数为( )
广告费用x(万元) | 2 | 3 | 4 | 5 | 6 |
销售轿车y(台数) | 3 | 4 | 6 | 10 | 12 |
A.17
B.18
C.19
D.20