Question

【题目】四边形为矩形，连接，，点在边上．

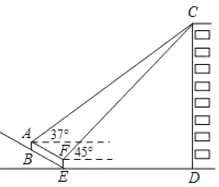
（1）如图①，若，，求的面积；

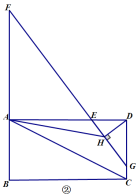
（2）如图②，延长至点，使得，连接并延长交于点，过点作于点，连接，求证：；

（3）如图③，将线段绕点旋转一定的角度（）得到线段，连接，点始终为的中点，连接．已知，直接写出的取值范围．

Answer 1

【答案】（1）；（2）证明见解析；（3）．

【解析】

（1）根据30°的直角三角形求CD和ED，再利用面积公式求△AEC的面积；

（2）作辅助线，构建全等三角形，证明△AFM≌△ADH，得AM＝AH，FM＝DH，则△MAH是等腰直角三角形，有MH＝AH，根据线段的和代入得结论；

（3）分别计算DN的最大值和最小值，连接AC和BD交于O，当DN在BD上，可得DN的最大值和最小值．

解：（1）如图1，在Rt△EDC中，

∵∠ECD＝30°，

∴，，

∴DC＝ECcos30°＝4×＝2，

∴AE＝2DC－ED＝4－2，

∴S△AEC＝×AE×DC＝（4－2）×2＝12－2；

（2）如图2，过A作AM⊥AH，交FG于M，

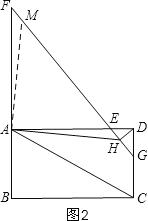
∴∠MAH＝∠MAD＋∠DAH＝90°，

又∵∠FAD＝∠MAD＋∠FAM＝90°，

∴∠FAM＝∠DAH，

∵AF∥CD，

∴∠F＝∠FGD

∵DH⊥EG，

∴∠DHE＝∠HDG＋∠FGD＝90°，

∠EDG＝∠EDH＋∠HDG＝90°，

∴∠FGD＝∠EDH，

∴∠F＝∠EDH，

又∵AF＝2CD，AD＝2CD，

∴AF＝AD，

∴△AFM≌△ADH，

∴AM＝AH，FM＝DH，

∴△MAH是等腰直角三角形，

∴MH＝AH，

∵FH＝MH＋FM，

∴FH＝AH＋DH；

（3）∵线段AE绕点A旋转一定的角度α（0°＜α＜360°）得到线段AE′，

∴E'的运动轨迹是一个以点A为圆心半径为4的圆，

连接AC，BD交于点O，

∵点O、N为AC、CE′的中点，

∴ON＝AE′＝2，

∵CD＝4，

∴BC＝AD＝2CD＝8，

在Rt△BCD中，，

∴

∴如图3，当DN在对角线BD上时，DN的长最小，DN＝OD－ON＝2－2，

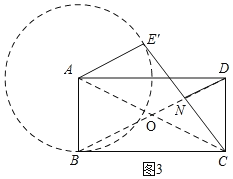
此时DN的值最小是2－2；

当α＞180°时，DN在BD上，如图4，DN最长，

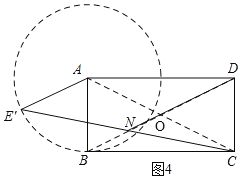
∴DN＝OD＋ON＝2＋2，

∵0°＜α＜360°，

∴2－2≤DN≤2＋2．