题目内容
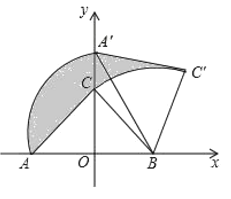
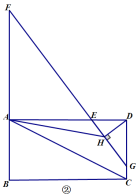
【题目】如图所示，在平面直角坐标系中，已知点A(－1，0)， B(0，
)，对△OAB连续作旋转变换，依次得到△1，△2，△3，△4，…，则△2019的直角顶点的坐标为______________．
【答案】(2019+673
，0)
【解析】
根据勾股定理列式求出AB的长，再根据第四个三角形与第一个三角形的位置相同可知每三个三角形为一个循环组依次循环，然后求出一个循环组旋转前进的长度，再用2019除以3，根据商为673可知第2019个三角形的直角顶点为循环组的最后一个三角形的顶点，求出即可．
∵点A(－1，0)， B(0，)，
∴AB＝
，
由图可知，每三个三角形为一个循环组依次循环，一个循环组前进的长度为：＋2＋1＝3+，
∵2019÷3＝673，
∴△2019的直角顶点是第673个循环组的最后一个三角形的直角顶点，
∵673×（3+）＝2019+673，
∴△2019的直角顶点的坐标为（2019+673，0）．
故答案为：（2019+673，0）．
练习册系列答案
相关题目
【题目】在学校组织的“文明出行”知识竞赛中，8（1）和8（2）班参赛人数相同，成绩分为A、B、C三个等级，其中相应等级的得分依次记为A级100分、B级90分、C级80分，达到B级以上（含B级）为优秀，其中8（2）班有2人达到A级，将两个班的成绩整理并绘制成如下的统计图，请解答下列问题：
（1）求各班参赛人数，并补全条形统计图；
（2）此次竞赛中8（2）班成绩为C级的人数为_______人；
（3）小明同学根据以上信息制作了如下统计表：
平均数（分） | 中位数（分） | 方差 | |
8（1）班 | m | 90 | n |
8（2）班 | 91 | 90 | 29 |
请分别求出m和n的值，并从优秀率和稳定性方面比较两个班的成绩；
