题目内容
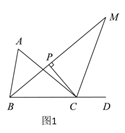
【题目】如图1，两个不全等的等腰直角三角形OAB和OCD叠放在一起，并且有公共的直角顶点O．
（1）在图1中，你发现线段AC，BD的数量关系是 ，直线AC，BD相交成 度角．
（2）将图1中的△OAB绕点O顺时针旋转90°角，这时（1）中的两个结论是否成立？请做出判断并说明理由．
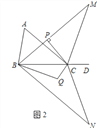
（3）将图1中的△OAB绕点O顺时针旋转一个锐角，得到图3，这时（1）中的两个结论是否成立？请作出判断并说明理由．
【答案】（1）AC=BD，90；
（2）成立，理由见解析；
（3）成立，理由见解析.
【解析】试题分析：（1）由图可知线段AC，BD相等，且直线AC，BD相交成90°角．（2）以上关系仍成立．延长CA交BD于点E，根据勾股定理可证得AC=BD，即可证明△AOC≌△BOD，根据两全等三角形对应角的关系，即可证明CE⊥BD．（3）结论仍成立．延长CA交OD于E，交BD于F，可证得△COA≌△DOB，同上即可得结论．
试题解析：(1)在图1中，线段AC，BD的数量关系是相等，直线AC，BD相交成90度角；
(2)(1)中结论仍成立；
证明如下：如图延长CA交BD于点E，
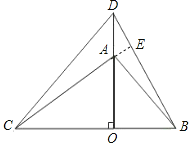
∵等腰直角三角形OAB和OCD，
∴OA=OB，OC=OD，
∵AC2=AO2+CO2,BD2=OD2+OB2，
∴AC=BD；
∴△DOB≌△COA(SSS)，
∴∠CAO=∠DBO，∠ACO=∠BDO，
∵∠ACO+∠CAO=90°，
∴∠ACO+∠DBO=90°,则∠AEB=90°,即直线AC,BD相交成90°角。
(3)结论仍成立；如图延长CA交OD于E，交BD于F，
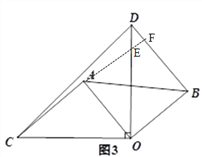
∵∠COD=∠AOB=90°，
∴∠COA+∠AOD=∠AOD+∠DOB，
即：∠COA=∠DOB，
∵CO=OD，OA=OB，
∴△COA≌△DOB(SAS)，
∴AC=BD，∠ACO=∠ODB；
∵∠CEO=∠DEF，
∴∠COE=∠EFD=90°，
∴AC⊥BD,即直线AC,BD相交成90°角。
