题目内容
【题目】如图,已知直线y=ax+b与双曲线y=![]() (x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(x>0)交于A(x1 , y1),B(x2 , y2)两点(A与B不重合),直线AB与x轴交于P(x0 , 0),与y轴交于点C.
(1)若A,B两点坐标分别为(1,3),(3,y2),求点P的坐标.
(2)若b=y1+1,点P的坐标为(6,0),且AB=BP,求A,B两点的坐标.
(3)结合(1),(2)中的结果,猜想并用等式表示x1 , x2 , x0之间的关系(不要求证明).
【答案】
(1)
解:∵直线y=ax+b与双曲线y=![]() (x>0)交于A(1,3),
(x>0)交于A(1,3),
∴k=1×3=3,
∴y=![]() ,
,
∵B(3,y2)在反比例函数的图象上,
∴y2=![]() =1,
=1,
∴B(3,1),
∵直线y=ax+b经过A、B两点,
∴![]() 解得
解得![]() ,
,
∴直线为y=﹣x+4,
令y=0,则x=4,
∴P(4,0)
(2)
解:如图,作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,
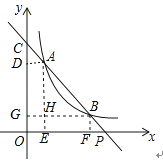
则AD∥BG∥x轴,AE∥BF∥y轴,
∴![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∵b=y1+1,AB=BP,
∴![]() =
=![]() ,
,
![]() =
=![]() =
=![]() ,
,
∴B(![]() ,
,![]() y1)
y1)
∵A,B两点都是反比例函数图象上的点,
∴x1y1=![]()
![]() y1,
y1,
解得y1=2,
代入![]() =
=![]() ,解得x1=2,
,解得x1=2,
∴A(2,2),B(4,1).
(3)
解:根据(1),(2)中的结果,猜想:x1,x2,x0之间的关系为x1+x2=x0.
【解析】(1)先把A(1,3)),B(3,y2)代入y=![]() span>求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
span>求得反比例函数的解析式,进而求得B的坐标,然后把A、B代入y=ax+b利用待定系数法即可求得直线的解析式,继而即可求得P的坐标;
(2)作AD⊥y轴于D,AE⊥x轴于E,BF⊥x轴于F,BG⊥y轴于G,AE、BG交于H,则AD∥BG∥x轴,AE∥BF∥y轴,得出![]() =
=![]() ,
, ![]() =
=![]() =
=![]() ,根据题意得出
,根据题意得出![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,从而求得B(
,从而求得B(![]() ,
, ![]() y1),然后根据k=xy得出x1y1=
y1),然后根据k=xy得出x1y1=![]()
![]() y1y1 , 求得y1=2,代入
y1y1 , 求得y1=2,代入![]() =
=![]() ,解得x1=2,即可求得A、B的坐标;
,解得x1=2,即可求得A、B的坐标;
(3)合(1),(2)中的结果,猜想x1+x2=x0 .

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( ) 
A.函数有最小值
B.对称轴是直线x= ![]()
C.当x< ![]() ,y随x的增大而减小
,y随x的增大而减小
D.当﹣1<x<2时,y>0
【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是___元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?