题目内容
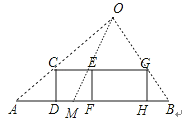
【题目】某兴趣小组开展课外活动.如图,A,B两地相距12米,小明从点A出发沿AB方向匀速前进,2秒后到达点D,此时他(CD)在某一灯光下的影长为AD,继续按原速行走2秒到达点F,此时他在同一灯光下的影子仍落在其身后,并测得这个影长为1.2米,然后他将速度提高到原来的1.5倍,再行走2秒到达点H,此时他(GH)在同一灯光下的影长为BH(点C,E,G在一条直线上).
(1)请在图中画出光源O点的位置,并画出他位于点F时在这个灯光下的影长FM(不写画法)
(2)求小明原来的速度。
【答案】
(1)
解:如图,
(2)
解:设小明原来的速度为xm/s,则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,EG=2×1.5x=3xm,BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,
∵点C,E,G在一条直线上,CG∥AB,
∴△OCE∽△OAM,△OEG∽△OMB,
∴![]() =
=![]() ,
,![]() =
=![]() ,
,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得x=1.5,经检验x=1.5为方程的解,
∴小明原来的速度为1.5m/s.
答:小明原来的速度为1.5m/s.
【解析】(1)利用中心投影的定义画图;
(2)设小明原来的速度为xm/s,则CE=2xm,AM=AF﹣MF=(4x﹣1.2)m,EG=2×1.5x=3xm,BM=AB﹣AM=12﹣(4x﹣1.2)=13.2﹣4x,根据相似三角形的判定方法得到△OCE∽△OAM,△OEG∽△OMB,列出方程求解即可
【考点精析】解答此题的关键在于理解相似三角形的应用的相关知识,掌握测高:测量不能到达顶部的物体的高度,通常用“在同一时刻物高与影长成比例”的原理解决;测距:测量不能到达两点间的举例,常构造相似三角形求解,以及对中心投影的理解,了解手电筒、路灯和台灯的光线可以看成是从一个点发出的,这样的光线所形成的投影称为中心投影;作一物体中心投影的方法:过投影中心与物体顶端作直线,直线与投影面的交点与物体的底端之间的线段即为物体的影子.

【题目】某种商品的进价为40元/件,以获利不低于25%的价格销售时,商品的销售单价y(元/件)与销售数量x(件)(x是正整数)之间的关系如下表:
x(件) | … | 5 | 10 | 15 | 20 | … |
y(元/件) | … | 75 | 70 | 65 | 60 | … |
(1)由题意知商品的最低销售单价是___元,当销售单价不低于最低销售单价时,y是x的一次函数.求出y与x的函数关系式及x的取值范围;
(2)在(1)的条件下,当销售单价为多少元时,所获销售利润最大,最大利润是多少元?