Question

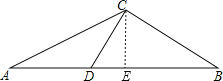
【题目】如图，在△ABC中，D为AB边上的一点，∠A＝36°，AC＝BC，AC2＝ADAB．

（1）求证：△ADC和△BDC都是等腰三角形；

（2）若AB＝1，求AC的值（精确到0.001）．

Answer 1

【答案】（1）见解析；（2）AC≈0.618．

【解析】

（1）由条件可证明△ACD∽△ABC，可得∠ACD＝∠B＝36°，可求得DC＝DA，且∠CDB＝∠DCB＝72°，可得BC＝BD，可证得结论；

（2）过C作AE⊥AB，利用等腰三角形的性质可知AE＝，在Rt△ACE中利用∠A的余弦值可求得AC．

（1）证明：∵AC2＝ADAB，

∴＝，且∠CAD＝∠BAC，

∴△ACD∽△ABC，

∴∠ACD＝∠B，

又∵AC＝BC，

∴∠A＝∠B＝36°，

∴∠A＝∠ACD＝36°，

∴AD＝CD，即△ADC为等腰三角形，

∴∠CDB＝2∠A＝72°，且∠B＝36°，

∴∠BCD＝∠CDB＝72°，

∴BC＝BD，

∴△BDC为等腰三角形；

（2）解：如图，过C作CE⊥AB于点E，

∵AC＝BC，

∴AE＝AB＝，

在Rt△ACE中，cos∠A＝，

∴＝cos36°，

∴AC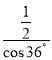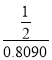＝≈＝0.618．

∴AC≈0.618．