题目内容
【题目】（本题满分10分）
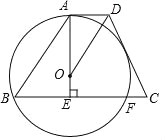
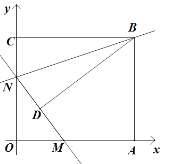
如图，矩形AOCB的顶点A、C分别位于x轴和y轴的正半轴上，线段OA、OC的长度满足方程|x-15|+=0(OB＞OC)，直线y=kx+b分别与x轴、y轴交于M、N两点，连接BN．将△BCN沿直线BN折叠，点C恰好落在直线MN上的点D处，且tan∠CBD=.
⑴ 求点B的坐标．
⑵ 求直线BN的解析式．
⑶ 将直线BN以每秒1个单位长度的速度沿y轴向下平移，求直线BN扫过矩形AOCB的面积S关于运动的时间t（0＜t≤13）的函数关系式.
【答案】（1）B（15，13）；（2）直线BN的解析式为y=
x+8；（3）S=
．
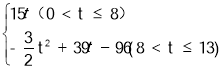【解析】
试题分析：（1）由非负数的性质可求得x、y的值，则可求得B点坐标；
（2）过D作EF⊥OA于点E，交CB于点F，由条件可求得D点坐标，且可求得
，结合DE∥ON，利用平行线分线段成比例可求得OM和ON的长，则可求得N点坐标，利用待定系数法可求得直线BN的解析式；
（3）设直线BN平移后交y轴于点N′，交AB于点B′，当点N′在x轴上方时，可知S即为BNN′B′的面积，当N′在y轴的负半轴上时，可用t表示出直线B′N′的解析式，设交x轴于点G，可用t表示出G点坐标，由S=S四边形BNN′B′﹣S△OGN′，可分别得到S与t的函数关系式．
试题解析：（1）∵|x﹣15|+
=0，
∴x=15，y=13，
∴OA=BC=15，AB=OC=13，
∴B（15，13）；
（2）如图1，过D作EF⊥OA于点E，交CB于点F，
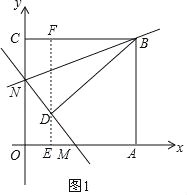
由折叠的性质可知BD=BC=15，∠BDN=∠BCN=90°，
∵tan∠CBD=
，
∴
，且BF2+DF2=BD2=152，解得BF=12，DF=9，
∴CF=OE=15﹣12=3，DE=EF﹣DF=13﹣9=4，
∵∠CND+∠CBD=360°﹣90°﹣90°=180°，且∠ONM+∠CND=180°，
∴∠ONM=∠CBD，
∴，
∵DE∥ON，
∴
，且OE=3，
∴
，解得OM=6，
∴ON=8，即N（0，8），
把N、B的坐标代入y=kx+b可得
，解得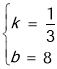
，
∴直线BN的解析式为y=x+8；
（3）设直线BN平移后交y轴于点N′，交AB于点B′，
当点N′在x轴上方，即0＜t≤8时，如图2，
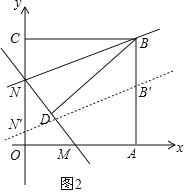
由题意可知四边形BNN′B′为平行四边形，且NN′=t，
∴S=NN′OA=15t；
当点N′在y轴负半轴上，即8＜t≤13时，设直线B′N′交x轴于点G，如图3，
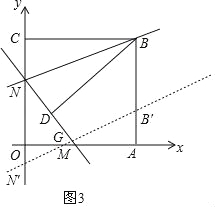
∵NN′=t，
∴可设直线B′N′解析式为y=x+8﹣t，
令y=0，可得x=3t﹣24，
∴OG=24，
∵ON=8，NN′=t，
∴ON′=t﹣8，
∴S=S四边形BNN′B′﹣S△OGN′=15t﹣
（t﹣8）（3t﹣24）=﹣
t2+39t﹣96；
综上可知S与t的函数关系式为S=．
