题目内容
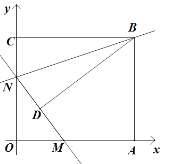
【题目】如图,梯形![]() 中,
中,![]() ,
,![]() 于
于![]() ,
,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,以点
,以点![]() 为圆心,
为圆心, ![]() 为半径的圆经过点
为半径的圆经过点![]() ,交
,交![]() 于另一点
于另一点![]() .
.
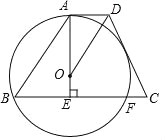
(1)求证:![]() 与
与![]() 相切;
相切;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)tan∠ABC=![]() .
.
【解析】
试题分析:(1)过点O作OG⊥DC,垂足为G.先证明∠OAD=90°,从而得到∠OAD=∠OGD=90°,然后利用AAS可证明△ADO≌△GDO,则OA=OG=r,则DC是⊙O的切线;
(2)连接OF,依据垂径定理可知BE=EF=12,在Rt△OEF中,依据勾股定理可知求得OF=13,然后可得到AE的长,最后在Rt△ABE中,利用锐角三角函数的定义求解即可.
试题解析:(1)过点O作OG⊥DC,垂足为G.
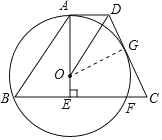
∵AD∥BC,AE⊥BC于E,∴OA⊥AD.∴∠OAD=∠OGD=90°.
在△ADO和△GDO中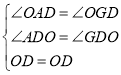 ,∴△ADO≌△GDO.∴OA=OG.∴DC是⊙O的切线.
,∴△ADO≌△GDO.∴OA=OG.∴DC是⊙O的切线.
(2)如图所示:连接OF.
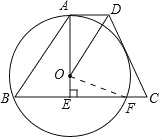
∵OA⊥BC,∴BE=EF=![]() BF=12.
BF=12.
在Rt△OEF中,OE=5,EF=12,∴OF=![]() =13.∴AE=OA+OE=13+5=18.∴tan∠ABC=
=13.∴AE=OA+OE=13+5=18.∴tan∠ABC=![]() =
=![]() .
.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目