Question

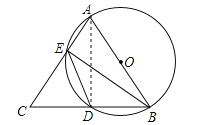
【题目】如图所示，AB＝AC，AB为⊙O的直径，AC、BC分别交⊙O于E、D，连结ED、BE．

（1）试判断DE与BD是否相等，并说明理由；

（2）如果BC＝6，AB＝5，求BE的长．

Answer 1

【答案】（1）见解析；（2）

【解析】试题分析：（1）可通过连接AD，AD就是等腰三角形ABC底边上的高，根据等腰三角形三线合一的特点，可得出∠CAD=∠BAD，根据圆周角定理即可得出∠DEB=∠DBE，便可证得DE=DB．

（2）本题中由于BE⊥AC，那么BE就是三角形ABC中AC边上的高，可用面积的不同表示方法得出ACBE=CBAD．进而求出BE的长．

试题解析：（1）DE=BD；连接AD，则AD⊥BC，在等腰三角形ABC中，AD⊥BC，∴∠CAD=∠BAD（等腰三角形三线合一），∴，∴DE=BD；

（2）∵AB=5，BD=BC=3，∴AD=4，∵AB=AC=5，∴ACBE=CBAD，∴BE=4.8．