Question

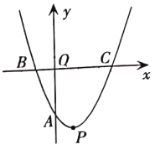
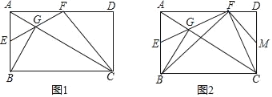
【题目】如图1，在矩形ABCD中，BG⊥AC交AC于点G，E为AB中点，EG的延长线交AD于点F，连接CF．

（1）若∠ABG＝30°，证明AF＝FD；

（2）如图2，若∠EFC＝90°，连接BF，FM⊥FB交CD于点M．

①证明：DM＝MC；

②求的值．

Answer 1

【答案】（1）见解析；（2）①见解析；②.

【解析】

（1）方法一：证明△AEF～△BAC，利用相似三角形的性质即可解决问题．

方法二：连接BD，证明EF∥BD即可解决问题．

（2）①方法一：利用相似三角形的性质证明即可．方法二：如图2，延长FM、BC交于点N，证明四边形DFCN是平行四边形即可．

②设AE＝x，AF＝y，求出AB2，AD2（用a表示），即可解决问题．

（1）∵∠ABG＝30°，∠ABC＝90°，

∴∠BAG＝60°，

在Rt△ABG中，AE＝BE，

∴∠AEF＝60°＝∠BAC，

又∵∠EAF＝∠ABC＝90°，

∴△AEF～△BAC，

∴，

又∵BC＝AD，

∴，

即AF＝FD．

（2）①∵∠EAF＝∠EFC＝∠FDC＝90°，

∴△EAF～△FDC，

∴，

同理可证△ABF～△DFM，

∴，

即，

∴，

∴，

∴DC＝2DM，

即DM＝CM，

②设AE＝x，AF＝y，

在Rt△ABG中，AE＝BE，

∴EA＝EG，

∴∠EAG＝∠EGA＝∠FGC，

又∵∠EAF＝∠EFC＝90°，

∴∠FAC＝∠FCA，

∴FA＝FC，

∵∠EAF＝∠EFC＝∠FDC＝90°，

∴△EAF～△FDC，

∴，

∴，

在Rt△DFC中，DF2+DC2＝FC2＝AF2

∴，

∴，

∴，

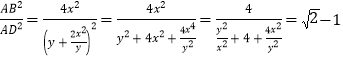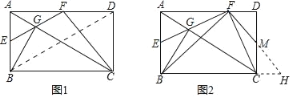
方法二：（1）如图1，连接BD．

在Rt△ABG中，∠BAG＝90°﹣30°＝60°，

∵矩形ABCD，

∴OA＝OB，

∴∠OBA＝∠OAB＝60°，

在Rt△ABG中，AE＝BE，

∴EA＝EG，

又∵∠OAB＝60°，

∴∠AEG＝60°＝∠ABO，

∴EF∥BD，

又∵AE＝BE，

∴AF＝FD

（2）①另证：如图2，延长FM、BC交于点N，

∵∠EAF＝∠EFC＝∠FDC＝90°，

∴△EAF～△FDC，

∴

∵∠EBC＝∠EFC＝90°，

∴∠FCN＝∠FEB

∵∠EFC＝∠BFN＝90°，

∴∠EFB＝∠CFN

∴△EFB～△CFN，

∴

又∵，

∴CN＝DF

又∵CN∥DF，

∴四边形DFCN是平行四边形，

∴DM＝MC．